Semestralny projekt

Úvod

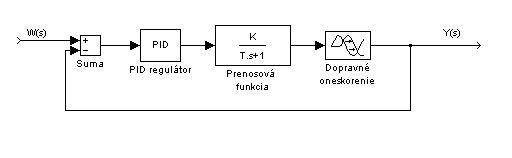
Existencia dopravného oneskorenia vo vstupno-výstupných vzťahoch je bežná vlastnosť mnohých technologických procesov. Výrobné zariadenia s časovým oneskorením často nemôžu byť riadené použitím bežných regulátorov navrhnutých bez zváženia prítomnosti dopravného oneskorenia. Regulačná odozva použitím týchto regulátorov smeruje k destabilizácii uzavretého regulačného systému.

Ako efektívny kompenzátor dopravného oneskorenia, špeciálne pre stabilný systém s dlhým dopravným oneskorením sa môže použiť Smithov prediktor. Konfigurácia regulačného systému, založená na Smithovom prediktore zahrňujúcom viaceré metódy nastavovania regulačných parametrov, bola vypracovaná mnohými autormi. Pri použití Smithovho prediktora sa predpokladá, že model procesu je známy. V skutočnosti sa dá dosť ťažko predpokladať, že parametre objektu riadenia sú úplne známe a nedochádza k ich odchýlkam. Pri zmene parametrov sa môžu použiť adaptívne algoritmy, ktoré prispôsobujú svoje parametre meniacej sa situácii.

Iný spôsob riešenia problému zmeny parametrov objektu predstavuje návrh pevného robustného regulátora, navrhnutého tak, že zmeny parametrov riadeného objektu neovplyvnia základné požiadavky regulačného obvodu.

V tomto projekte je riešená úloha návrhu takého robustného regulátora pre daný (nominálny) prenos prvého rádu s dopravným oneskorením, ktorý zabezpečí stabilitu regulačného obvodu a asymptotickú konvergenciu regulačnej odchýlky k nule aj pre perturbovaný prenos, ktorý sa odlišuje od nominálneho. Dopravné oneskorenie je vhodne aproximované.

Na ovplyvnenie robustnosti a regulačného chovania sa používa skalárny parameter m> 0, ktorý vyplýva z normy , kde S je citlivostná funkcia. Parametre regulátora sa získajú riešením diofantických rovníc.

2. Dopravné oneskorenie

Súčasťou dynamiky prevažnej väčšiny chemickotechnologických a biotechnologických procesov je dopravné oneskorenie. Dlhé dopravné oneskorenie najčastejšie vzniká ako dôsledok transportných javov, ktoré prebiehajú v riadených objektoch. Krátke vzniká napr. pri riadení koncentračných sústav.

Dopravné oneskorenie sa pri snahe riadiť technologické procesy často stáva problémom, keďže mnoho klasických metód pri snahe riadiť sústavy s dopravným oneskorením havaruje. Prítomnosť dopravného oneskorenia v systéme pri spätnoväzbovom riadení má nepriaznivý vplyv na stabilitu systému riadenia. Sklon k nestabilite pritom rastie s veľkosťou dopravného oneskorenia. V posledných rokoch sa touto problematikou zaoberá návrh robustných regulátorov, teda pevných regulátorov navrhnutých tak, že zmeny parametrov riadeného objektu neovplyvnia základné požiadavky regulačného obvodu (stabilitu, asymptotické sledovanie, kompenzáciu poruchy a pod.).

Treba poznamenať, že veľkosť dopravného oneskorenia a tým aj jeho významnosť nie je daná jeho absolútnou hodnotou, ale pomerom k časovým konštantám riadeného objektu.

Vplyv dopravného oneskorenia v riadenom objekte na vlastnosti uzavretého obvodu si môžeme aspoň naznačiť, ak použijeme štandardný spätnoväzbový obvod.

Obr. 2.1: Štandardný spätnoväzbový obvod

3. Návrh robustného riadenia

Základná úloha návrhu robustného riadenia je vybrať z množiny stabilizujúcich regulátorov, určených k danému prenosu G (nominálny prenos) také regulátory, ktoré spĺňajú zadané podmienky i pre perturbovaný prenos G^", ktorý sa od nominálneho odlišuje.

Algoritmus spätnoväzbového riadenia a kritérium kvality riadenia sú determinované matematickým modelom procesu, meracím a akčným členom. Pri návrhu algoritmu spätnoväzbového riadenia budeme vychádzať z blokovej schémy:

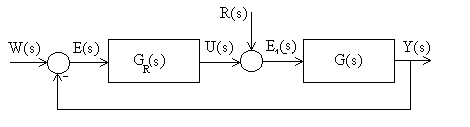
G(s) je prenos riadeného objektu, G_R(s) je prenos regulátora, W(s) je obraz žiadanej veličiny, R(s) je obraz poruchovej veličiny, Y(s) je obraz výstupnej veličiny. Žiadaná a poruchová veličina sú vstupné veličiny spätnoväzbového systému.

Návrh spätnoväzbového riadenia spočíva v určení štruktúry regulátora a výberu jeho konštánt tak, aby sme dosiahli v určitom zmysle optimálnu odozvu procesu. Určiť štruktúru regulátora a zvoliť jeho vhodné konštanty znamená vlastne určiť vhodný prenos G_R(s).

Od optimálneho algoritmu spätnoväzbového riadenia sa vyžaduje, aby zaistil splnenie nasledovných požiadaviek:

Systém spätnoväzbového riadenia musí byť stabilný.

Systém spätnoväzbového riadenia musí eliminovať vplyv porúch.

Systém spätnoväzbového riadenia musí zabezpečiť optimálne sledovanie žiadanej veličiny.

Pri riadení sa musí dosiahnuť nulová trvalá odchýlka riadenia.

Akčné zásahy pri riadení musia byť akceptovateľné pre proces.

Algoritmus spätnoväzbového riadenia musí byť schopný zohľadniť chyby predpokladaného modelu procesu.

4. Návrh regulátora.

Úloha návrhu regulátora sa obyčajne formuluje tak, že pre daný prenos G(s) je treba nájsť taký prenos G_R(s), aby uzavretý systém riadenia bol vnútorne stabilný a realizovateľný a odchýlka riadenia e pri spätnoväzbovom riadení po skokovej zmene w musí v čase konvergovať k nule.

Regulátor s prenosom G_R(s) navrhneme nasledovne. Prenosová funkcia G(s) môže byť vyjadrená ako podiel dvoch nesúdeliteľných polynómov B(s) a A(s). Prenosovú funkciu môžeme písať aj v zlomkovom tvare:

pričom st B<st A, st M₁=st A. st(.) označuje stupeň polynómu. M₁ je stabilný polynóm.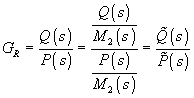

Pre regulátor môžeme napísať funkciu:

pričom platí:

Rovnica sa nazýva podmienková rovnica stability spätnoväzbového systému. Prenosovú funkciu regulátora G_R(s) určíme z diofantickej rovnice:

Riešenie rovnice spočíva v určení polynómov P(s) a Q(s) tak, aby táto rovnica bola splnená. Riešenie rovnice existuje, ak najväčší spoločný deliteľ polynómov A(s) a B(s) delí polynóm M(s)=M₁(s)M₂(s).

Názov diofantická rovnica je podľa matematika Diophantosa. Diofantické rovnice sú lineárne rovnice s polynómami.

Ak má diofantická rovnica riešenie x₀,y₀, potom ich má nekonečne veľa a obecné riešenie má tvar:

kde t je ľubovoľný polynóm.

Stupne polynómov P(s) a Q(s), ktoré vlastne určujú štruktúru regulátora sú závislé od modelu procesu. Čiže regulátor a kvalita riadenia je rozhodujúcim spôsobom determinovaná chemicko-inžinierskym návrhom procesu.

5. Citlivostná funkcia systému

Uvažujeme, že prenos otvorenej slučky je G(s) G_R(s)=L(s)

Potom citlivostná funkcia (dynamický činiteľ regulácie) má tvar

Pre dané

sa môže použiť norma:

odhad maxima z n bodov w _i, i´1,… N

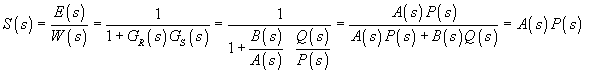
6. Posudzovanie kvality spätnoväzbového riadenia

Získané prechodové charakteristiky sa vyhodnocovali na základe viacerých kritérií:

trvalá regulačná odchýlka riadenia - je to rozdiel žiadanej veličiny a výstupnej veličiny procesu v nekonečnom čase.

w(t) je žiadaná veličina

y(t) je riadená veličina

maximálny prekmit výstupnej veličiny - y_M je to rozdiel maximálnej hodnoty výstupnej veličiny a žiadnej veličiny v prípade úlohy sledovania, ak sa žiadaná veličina v čase t = 0 zmení skokom. Vo väčšine prípadov je snaha, aby tento prekmit bol čo najmenší. Maximálne preregulovanie je dané vzťahom:

čas regulácie - je to čas, za ktorý dosiahne výstupná veličina po skokovej zmene w, resp. r žiadanú veličinu s určitou presnosťou. Z hľadiska času regulácie je lepšie také riadenie, pri ktorom je doba prechodového javu menšia.

integrálne kritériá kvality - cieľom je dosiahnuť čo najmenší integrál absolútnej, resp. kvadratickej odchýlky riadenia. Integrál absolútnej hodnoty odchýlky riadenia (Integral of the absolute value of the error):

Integrál kvadratickej odchýlky riadenia (Integral of the square error):

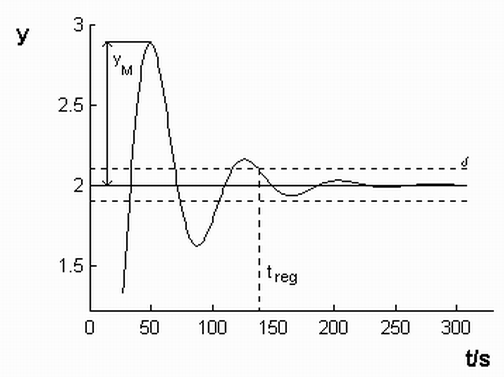
Obr. 6.1: Prechodová charakteristika so znázornenými kritériami kvality.

7. Aproximácia prenosovej funkcie s dopravným oneskorením.

Ak riadenú sústavu môžeme popísať ako systém prvého rádu s dopravným oneskorením, prenosovú funkciu môžeme vyjadriť vo všeobecnom tvare:

kde K- zosilnenie,

T- časová konštanta,

d- dopravné oneskorenie.

Výraz s dopravným oneskorením e^-ds môže byť nahradený rôznymi výrazmi. V tomto projekte sú popísané tri aproximácie dopravného oneskorenia pomocou prvých členov Taylorovho rozvoja a Padého aproximácia:

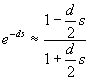
V prvom kroku dopravné oneskorenie e^-ds nahradíme prvým členom Taylorovho rozvoja polynómu

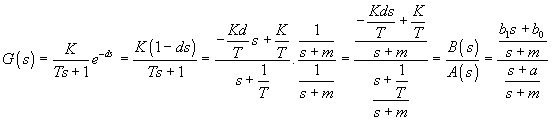
a dosadením upravíme prenosovú funkciu

Z rovnosti vyjadríme koeficienty

Pre túto sústavu odvodíme spätnoväzbový regulátor a jeho prenos upravíme podobne do tvaru:

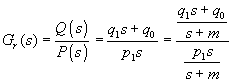
Je to prenos prvého rádu, pre ktorý môžeme použiť PI regulátor. Pre tento platí:

Porovnaním obidvoch vzťahov získame koeficienty prenosu regulátora:

Stabilizujúci spätnoväzbový regulátor je viazaný rovnicou

A(s)P(s)+B(s)Q(s)=1

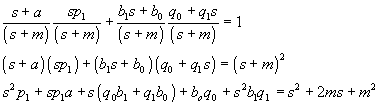
Do rovnice dosadíme polynómy

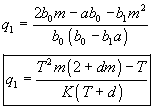
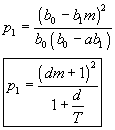
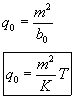
a porovnaním pravej a ľavej strany môžeme vyjadriť

Ako druhú aproximáciu dopravného oneskorenia použijeme prvé členy Taylorovho rozvoja menovateľa.

Regulátor má tvar:

Ide o prenos druhého rádu, pre ktorý použijeme PID regulátor. Analogickými úpravami získame jeho koeficienty:

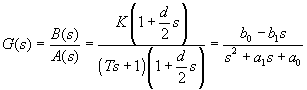
Treťou použitou aproximáciou je Padého náhrada:

Regulátor má tvar:

Vyjadríme jeho koeficienty:

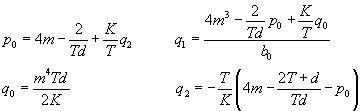
8. Experimentálna časť

Ak veľkosť perturbácie nie je známa, hľadá sa medzi stabilizujúcimi regulátormi taký, ktorý minimalizuje citlivostnú funkciu S(s) [2], [4]

Robustný regulátor bol navrhovaný pre proces s parametrami: d = 5, K = 1.25, T = 2. Pre tento prenos zobrazuje obrázok citlivostnú funkciu s minimom min˝ S˝ =1.49, m = 0.16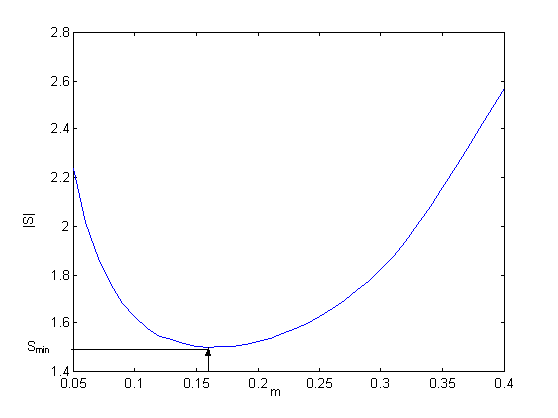

Obr. 8.1: Citlivostná funkcia navrhnutého prenosu.

V [2] je pre charakteristickú citlivosť

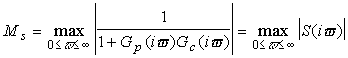
doporučená hodnota medzi 1.3 až 2. V takomto prípade by pre m platilo mÎ < 0.06, 0.33> .

Pre m=0.16 je P = - 0.0257, I = 0.0442.

Keďže zosilnenie regulátora má byť kladné, musí platiť:

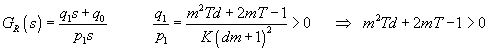
Riešením kvadratickej rovnice dostávame:

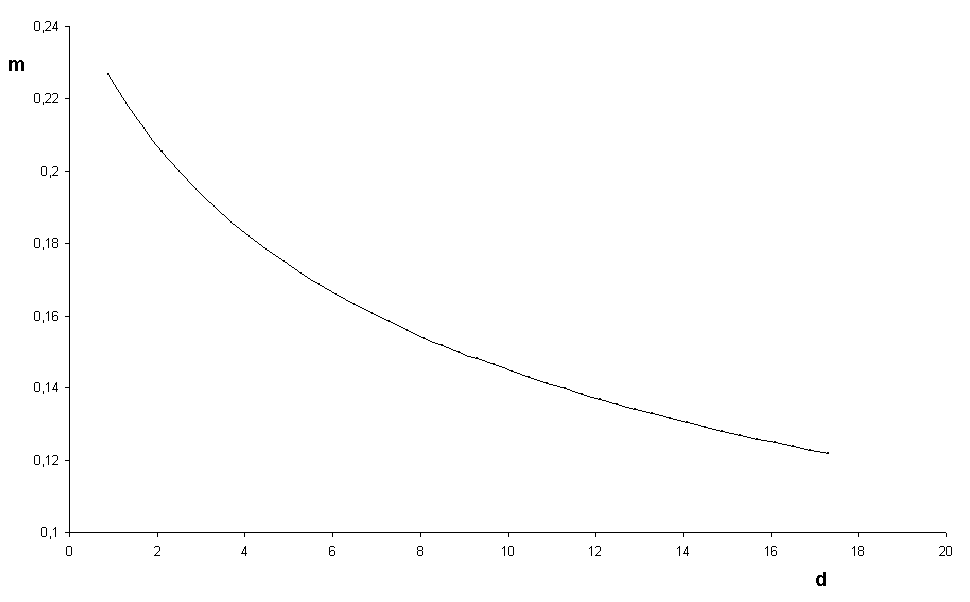
Obr. 8.2: Kritické hodnoty m v závislosti od dopravného oneskorenia d.

Iba pre m, ktoré spĺňa uvedený vzťah, je P kladné. Teda pre náš systém platí

m > 0.1742. Pri návrhu regulátora bolo vybrané m=0.18.

Pre m=0.18 je P = 0.0098, I = 0.0503

Pre každú náhradu boli odvodené parametre regulátora. V prostredí matlab+simulink bola použitá schéma na simulovanie správania sa systému pri nastavených parametroch. Skúmali sa všetky tri aproximácie a zo spoločného porovnania prechodových charakteristík sa vybrala najvhodnejšia aproximácia.

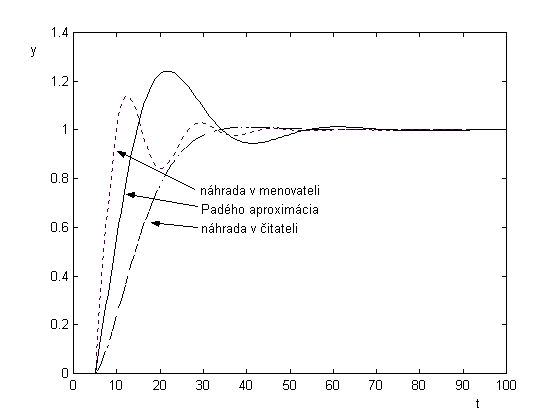
Obr. 8.3: Porovnanie prechodových charakteristík systémov s rôznymi

aproximáciami dopravného oneskorenia

Z grafu vidieť, že najlepšie sa systém správal pri náhrade e^-ds=1-ds v čitateli prenosu, kedy je navrhovaný PI regulátor.

Pre navrhnutý regulátor sa skúmali intervaly, v ktorých sa môžu meniť parametre riadenej sústavy, teda zosilnenie, časová konštanta a dopravné oneskorenie tak, že sa menil postupne vždy jeden parameter, kým sa sústava nestala nestabilnou..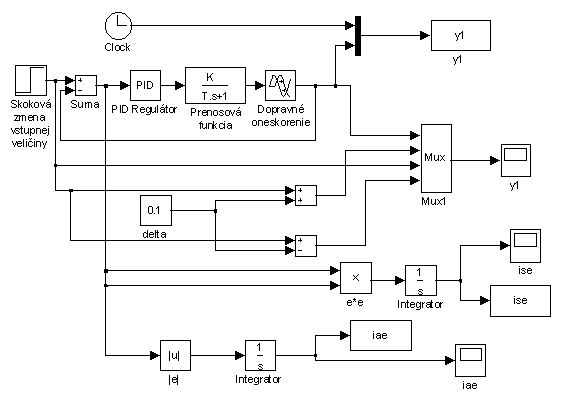

Obr. 8.4: Schéma zapojenia sústavy s dopravným oneskorením, regulovanej

PID regulátorom.

Získané prechodové charakteristiky systému sa vyhodnotili opísanými kritériami kvality.

Na prvých štyroch obrázkoch sú prechodové charakteristiky pri zväčšovaní dopravného oneskorenia. Priebeh sa so zväčšovaním d rozkmitával a pri d=26 je systém nestabilný.

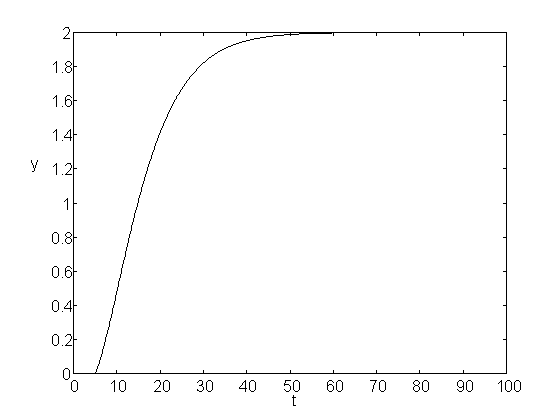
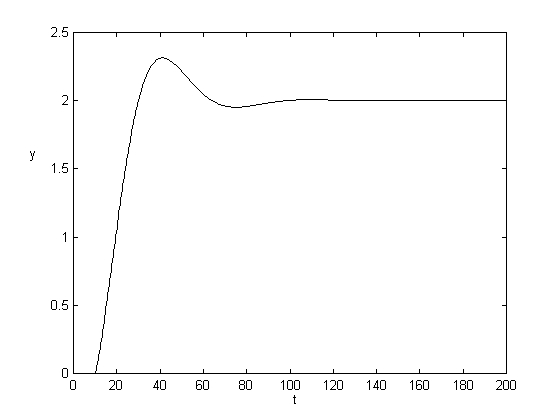
d = 5, K = 1.25, T = 2 d = 10, K = 1.25, T = 2

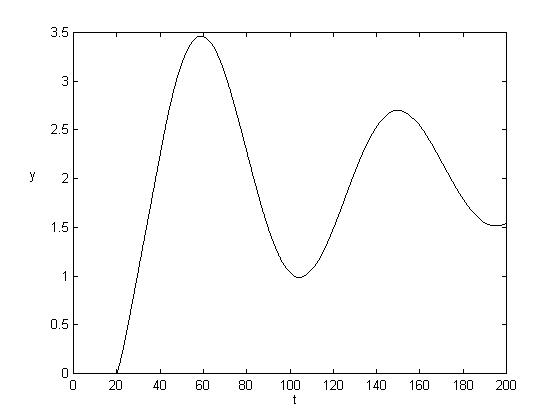
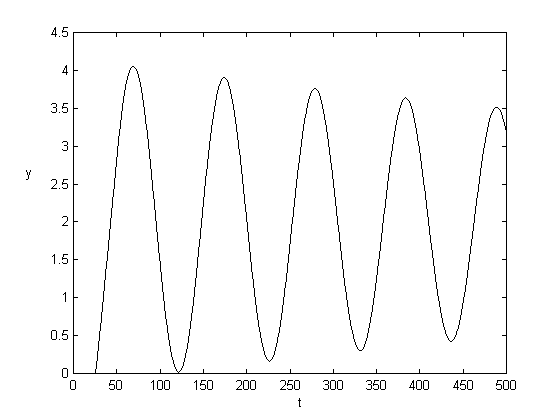
d = 20, K = 1.25, T = 2 d = 25, K = 1.25, T = 2

d	y_max	t_max	t_reg	e	ise	iae
1	---	---	46,25	0	37,9443	33,8359
5	---	---	34,59	0	48,3526	33,8359
10	2,31	41,20	56,55	0	67,7175	46,6191
15	2,87	49,20	137,94	0	103,4947	85,1620
20	3,46	58,80	383,54	0	199,0200	195,5864
25	4,05	68,86	---	0	---	---
26	Nestabilný

Na ďalších troch obrázkoch sú prechodové charakteristiky pre dopravné oneskorenie d=5 a rôzne hodnoty časovej konštanty T. So zväčšovaním T sa zväčšoval aj čas regulácie, ale ani pri veľkých hodnotách časovej konštanty nebol priebeh nestabilný.

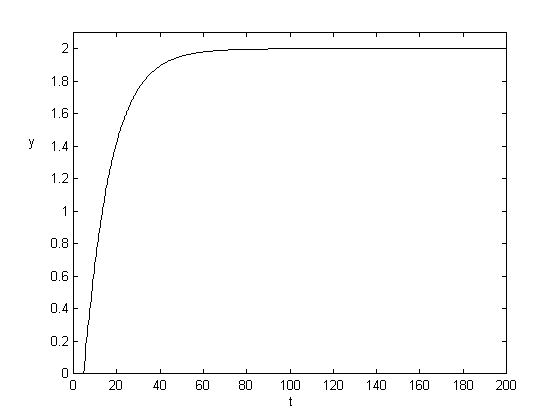
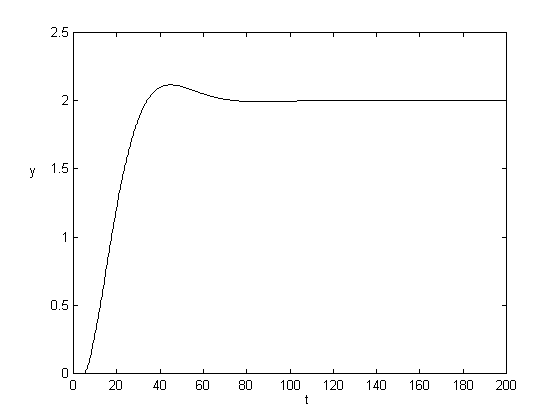
d = 5, K = 1.25, T = 0.2 d = 5, K = 1.25, T =5

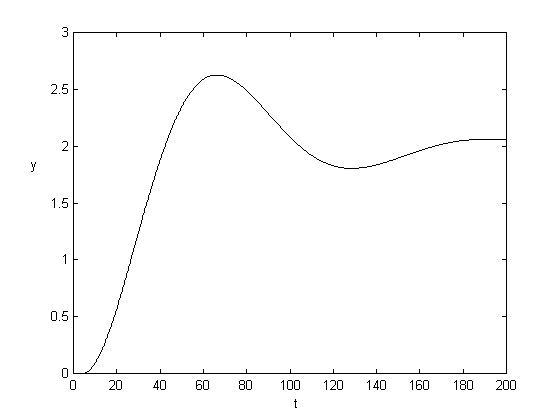
d = 5, K = 1.25, T = 20

T	y_max	t_max	t_reg	e	ise	iae
1	---	---	38,21	0	45,7302	33,8359
5	2,12	44,8	50,74	0	56,2219	38,9161
10	2,35	52,0	74,29	0	69,3404	54,2127
15	2,51	59,6	127,19	0	82,4593	70,4950
20	2,63	66,4	150,80	0	95,5782	86,9968
25	2,72	72,6	169,30	0	108,6971	103,5819

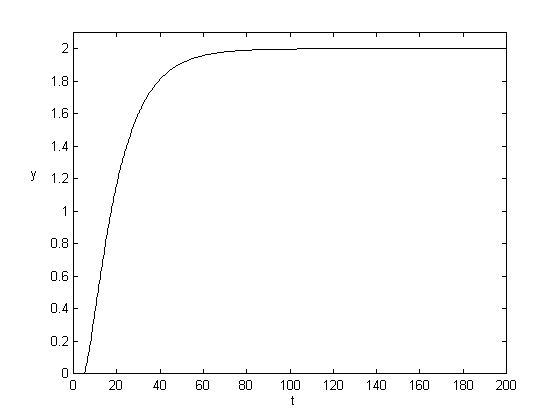
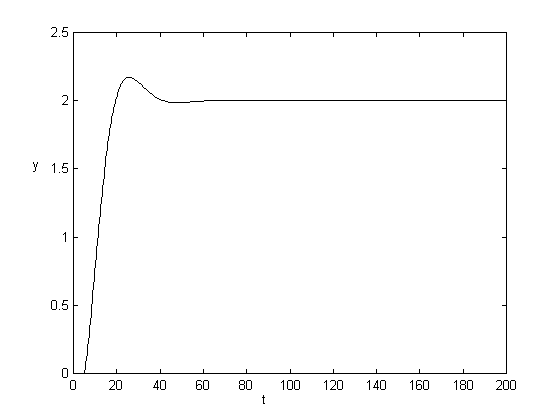
d = 5, K = 1, T = 2 d = 5, K = 2, T = 2

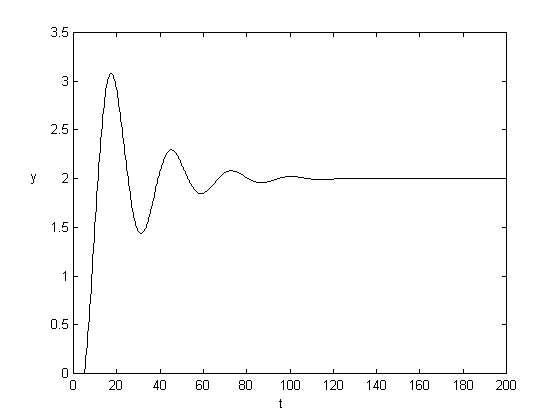
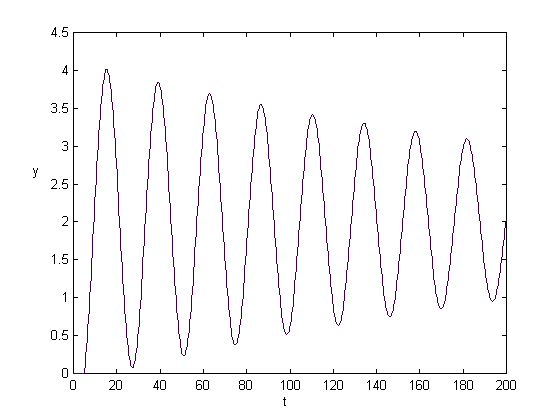
d = 5, K = 4, T = 2 d = 5, K = 6, T = 2

Pri zmene zosilnenia K sa so stúpajúcim zosilnením priebeh rozkmitáva. Pri K=6 je systém na hranici stability, ako vyplýva z ďalších štyroch predchádzajúcich obrázkov .

K	y_max	t_max	t_reg	e	ise	iae
1	---	---	48,46	0	56,2196	42,2949
2	2,17	25,60	32,80	0	37,8649	25,3824
4	3,08	17,20	63,00	0	40,5673	36,5828
5	3,55	16,00	131,53	0	61,7052	64,0084
6	4,01	15,20	824,27	0	312,2395	359,5614
7	nestabilný

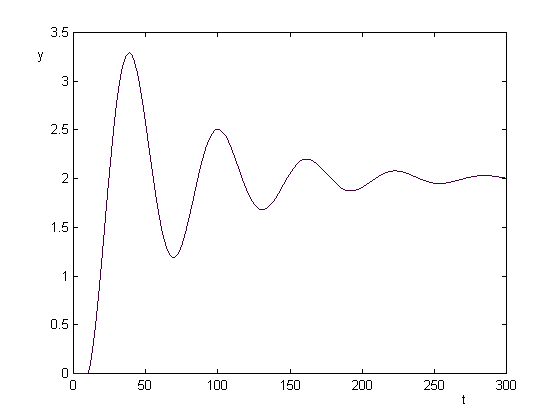
Obr. 8.5: Perturbovaný prenos: K=2, T=5, d=10.

9. Záver

V reálnych systémoch je výskyt krátkeho dopravného oneskorenia pomerne častý. Preto je dôležité správne navrhnúť regulátor aby sa zabezpečila stabilita regulačného obvodu. Existuje mnoho metód na návrh regulátorov.

Projekt sa zaoberal návrhom robustného regulátora pre zadanú sústavu opísanú prenosom s parametrami K=1.25, T=2, d=5. Dopravné oneskorenie bolo nahradené pomocou prvých členov Taylorovho rozvoja a Padého aproximácie:

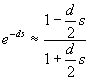
Z experimentov vyplynulo, že vhodnou náhradou je náhrada najjednoduchšia a to náhrada v čitateli prenosu (Obr. 8.3), kedy sa použije PI regulátor.

Pre túto aproximáciu boli odvodené parametre regulátora pomocou riešenia diofantických rovníc. Regulátor s odvodenými parametrami sa môže použiť aj pre perturbovaný prenos, keď sa parametre regulovanej sústavy menia v rozsahu: KÎ (1;7) , TÎ (1;25) , dÎ (1;25). (Obr. 8.5)

10. Použitá literatúra

[1] Mikleš, J., Dostál, P., Mészáros, A.: Riadenie technologických procesov, STU

Bratislava, 1994

[2] Ĺström, K. J., Hägglund, T. : PID Controllers: Theory, Desing and Tuning.

Instrument Society of America, Research Triangle Park, NC, second edition 1995

[3] Prokop, R., Prokopová, Z.: Robust Tuning of PID-like Controllers, Selected

Topics in Modelling and Control, Vol. 2, pp. 28-33, 1999

[4] Dostál, P., Prokop, R., Bobál, V.: Polynomial Desing of Simple Controllers for

Time Delay Systems, Selected Topics in Modelling and Control, Vol. 3,pp. 74-80, 2002

[5] Babatunde A. Ogunnaike, W. Harmon Ray.: Process, Dynamics, Modeling and

Control. Oxford University Press, Inc., 1994