Bakalársky projekt
Základné pojmy fuzzy teórie
Základom môjho projektu bolo navrhnúť model technologického procesu prostredníctvom fuzzy toolboxu programu Matlab. V prvom rade by som chcela vysvetliť základné pojmy fuzzy teórie.Fuzzy logika - schopnosťou fuzzy logiky je matematicky podchytiť informácie vyjadrené slovne. Umožňuje pracovať s nejednoznačnými pojmami používanými v ľudskej reči. Umožňuje počítaču pochopiť čo znamená veľa, málo.. na základe porovnania.
Fuzzy množiny - Teória fuzzy množín spočíva v zavedení tzv. stupňa príslušnosti prvku k množine, ktorá môže nadobúdať hodnoty z intervalu na rozdiel od klasických teórií množín, kde každý prvok do množiny buď patrí alebo nepatrí.
Lingvistická premenná - Je to premenná, ktorej hodnoty sú výrazmi nejakého jazyka.
Funkcia príslušnosti - Charakterizuje stupeň, s ktorým daný prvok patrí do príslušnej množiny a to od hodnoty 0, keď prvok do množiny určite nepatrí, až do hodnoty 1 kedy prvok do množiny určite patrí.
Fuzzyfikácia - Proces priraďovania meraných hodnôt vstupujúcich veličín do fuzzy množín pomocou funkcií príslušnosti sa označuje ako fuzzyfikácia.
Defuzzyfikácia - proces "aproximácie neostrých termov" ostrou hodnotu.
späť na začiatok
Matematický model chemického reaktora
Ja som si vybrala ako technologický proces chemický reaktor, ktorý mi bol blízky zo základov automatizácie. Matematické modely chemických reaktorov dajú získať len s použitím mnohých zjednodušujúcich predpokladov. Jedným z nich je linearizácia nelineárnych vzťahov. Keďže matematický opis reaktora tvorili diferenciálne rovnice, ktoré nebolo treba linearizovať, na vytvorenie modelu chemického reaktora stačila s - funkcia. Na obrázku vidíme schému modelu chemického reaktora vytvoreného prostredníctvom programu Matlab.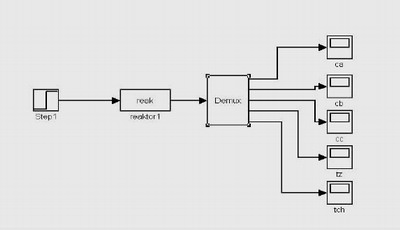
späť na začiatok
Anfis štruktúra
Program Matlab ponúka dva typy fuzzy modelov: model typu Mamdani a model typu Sugeno. Charakteristickou vlastnosťou modelu typu Mamdani je fuzzy výstup. Naopak, model typu Sugeno má na výstupe ostré hodnoty. Je výstupom z Anfis štruktúry, ktorá je súčasťou matlabu, preto som ďalej pracovala práve s týmto modelom. Ako som už spomínala používala som model typu Sugeno, pretože je výstupom zo štruktúry Anfis, ktorá je súčasťou programu matlab. Anfis využíva schopnosť hybridného určenia algoritmov k identifikácii parametrov funkcií príslušnosti jednoduchého výstupu. Pre "tréning" FIS členov na určenie parametrov funkcií príslušnosti sa používa kombinácia metódy najmenších štvorcov a metódy spätného šírenia. Jej výhodou je to, že jej výsledkom je práve neuro fuzzy model typu Sugeno. Stlačením load data som schopná načítať uložené údaje - v mojom prípade to boli hodnoty Tz. Opäť je možné navoliť počet funkcií príslušnosti (PFP), typ funkcie príslušnosti (FP) pre vstup aj výstup a po trenévaní údajov nám Anfis vydá testovacie údaje podľa FIS vzoru. späť na začiatokVplyv zmeny PFP na jednotlivé priebehy
Jednou z mojich úloch bolo sledovať vplyv zmeny PFP na jednotlivé priebehy. Hore je neuro-fuzzy model chemického reaktora typu Sugeno pri zadaní počtu funkcií príslušnosti 3 a typu FP gaussmf. Dole je neuro fuzzy model typu Sugeno ale s PFP rovným 7. Vplyv PFP je vidieť len v lepšom nábehu pri PFP rovný 7. Inak je priebeh takmer rovnaký. V našom jednoduchom priebehu nemá zvyšovanie PFP takmer žiadny význam.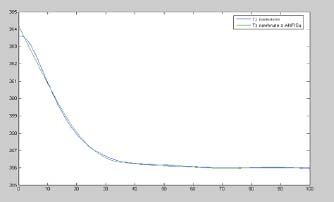
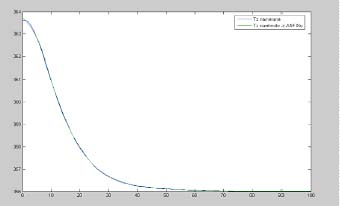
späť na začiatok
Vplyv zmeny PFP na zhodu modelu
Vytvorila som ďalšie modely, pričom na tomto modeli som opäť zisťovala vplyv zmeny PFP na zhodu modelu, ale s použitím zložitejšej sinusovej funkcie y = sin(2*x)./exp(x/5). V uvažovaných prípadoch vyššia hodnota PFP znamená väčší počet pravidiel, a tým je podmienená lepšia presnosť modelu. Na hornom obrázku celý priebeh takmer identicky kopíruje trénované údaje. Naopak, pri dolnom obrázku a pri hodnote PFP 3 je priebeh horší, zhoda s trénovanými údajmi je takmer minimálna. Z toho vyplýva, že zvyšovanie PFP má v našom prípade na priebeh veľký vplyv.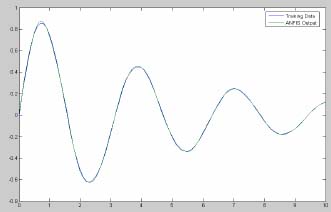
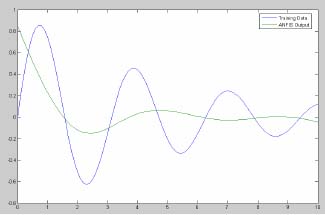
späť na začiatok
Model s dvoma vstupmi a jedným výstupom
Základom práce s daným modelom, ktorý je opísaný ako sústava 1. rádu s dopravným oneskorením je schéma systému, kde neuvažujeme iba časový priebeh výstupných veličín, ale na vstupe je 5 skokových zmien vstupnej veličiny u.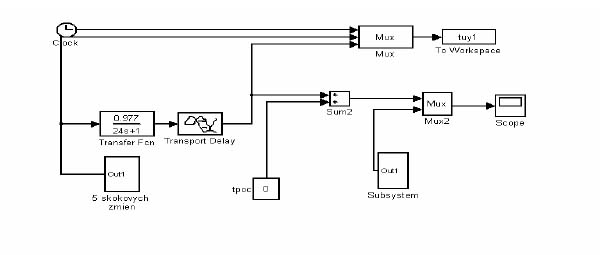
Výsledný priebeh y je zobrazený na tomto obrázku.
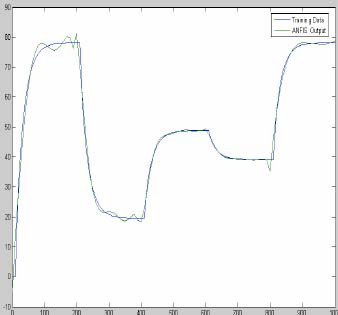
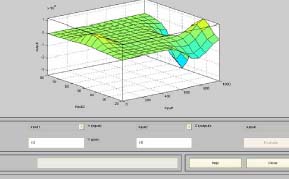
Keďže máme dva vstupy a pre každý vstup uvažujeme 5 funkcií príslušnosti typu gaussmf, počet pravidiel bude 5x5=25 pravidiel.
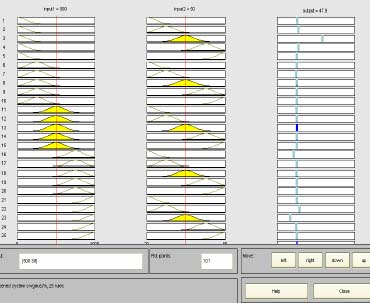
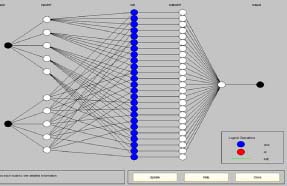
Hore je zobrazený výsledný povrch, samozrejme trojrozmerne, kdeže máme 2 vstupy a 1 výstup. Štruktúra je zobrazená na dolnom obrázku a vidieť že je zložitejšia práve kvôli prepájaniu vstupov s jednotlivými pravidlami.
späť na začiatok
Záver
Svoj bakalársky projekt som uviedla len vo forme prezentácie, ktorú som použila na štátnu skúšku. V prípade záujmu je možné si celý bakalársky projekt stiahnuť vo forme pdf.Kapitoly:
späť na začiatok