SLOVENSKÁ TECHNICKÁ UNIVERZITA V BRATISLAVE

Fakulta chemickej a potravinárskej technológie

Katedra informatizácie a riadenia procesov

SEMESTRÁLNY PROJEKT

TESTOVANIE OPTIMALIZAČNEJ METÓDY V PROSTREDÍ MATLAB

Autor projektu: Katarína Rybárová

Vedúci projektu: Doc. Ing. Ján Dvoran, PhD.

Úvod

Cieľom tohto semestrálneho projektu bola voľba vhodnej optimalizačnej metódy, jej testovanie pri riešení konkrétnych optimalizačných problémov a určenie oblasti, v ktorej je možné danú zvolenú optimalizačnú metódu použiť. Projekt, je spracovaný podľa zadania tak, že je prehľadne rozdelený do troch tematických celkov popísaných v 4 kapitolách.

Prvá, teoretická časť práce, je uvedená v kapitolách 1 a 2 sa zaoberá úvodom do zvolenej problematiky optimalizácie. Je v nej uvedené aj rozdelenie optimalizačných problémov a optimalizačných metód. V druhej kapitole je podrobnejšie rozobraná zvolená optimalizačná metóda – Lineárne programovanie.

Druhú časť tvorí analýza a popis optimalizačných programov z prostredia MATLAB, ktoré sú použité na testovanie zvolenej optimalizačnej metódy a konkrétnych optimalizačných úloh. V rámcii tejto analýzy sú uvedené aj jednoduché úlohy na, ktorých je rozobraný mechanizmus daného programu.

V tretej, poslednej, časti sú uvedené konkrétne optimalizačné úlohy, na ktorých bola optimalizačná metóda testovaná. V kapitole 4 je tiež uvedená oblasť použiteľnosti zvolenej optimalizačnej metódy.

V závere sú zhrnuté dosiahnuté výsledky, zistené pomocou danej optimalizačnej metódy a záverečné hodnotenia vyplývajúce z praktických výsledkov testovania optimalizačnej metódy.

1 ÚVOD DO OTPIMALIZÁCIE

V každom okamihu sa treba rozhodovať: Čo urobím? Aké mám možnosti? Akú cenu má dané rozhodnutie a čo ním získam?

Väčšina činností sa vykonáva tak, aby nimi bol dosahovaný čo najlepší možný výsledok. Nejde len o ľudské a ekonomické činnosti, ale aj priemyselné zariadenia a stroje. Technologické procesy, experimenty a programy, sú nastavované na dosahovanie čo najlepšieho a najvyššieho výkonu, po zohľadnení nákladov a podmienok. Väčšinu týchto činností, problémov možno riešiť matematicky, vytvorením optimalizačnej úlohy.

Optimalizácia je všetko, čím získavame najlepšie, najvhodnejšie, najvyhovujúcejšie podmienky a riešenia situácií, problémov, programov, plánov a pod. Je využiteľná nielen na riešenie momentálne vzniknutých problémov, ale zohľadňuje sa najmä pri tvorbe plánov, projektov a stratégií. Takisto je vhodná na analýzu toho, čo už bolo vytvorené.

Optimalizácia je prístup, ktorým sa dosahuje zisk po zohľadnení všetkých faktorov, ktoré ovplyvňujú naše rozhodnutia. Väčšina optimalizačných problémov je komplexná, vyžaduje rozhodnutia, ktoré sú čo najvhodnejšie, teda optimalizované.

Z ekonomického hľadiska sa optimalizáciou rozumie dosahovanie čo najvyššieho zisku pri, podľa možností, čo najnižších nákladoch.

Z matematického hľadiska pod optimalizáciou možno rozumieť aktivitu, ktorej cieľom je nájsť najvhodnejšie, t.j. optimálne riešenie danej matematickej úlohy (vyhľadávaním extrémov funkcií).

Optimalizačných úloh a problémov je veľmi veľa, je teda veľmi užitočná ich klasifikácia. Dôležitý je hlavne tvar účelovej funkcie a vlastnosti obmedzujúcich podmienok (linearita, nelinearita, ohraničenosť a pod.). Na základe toho možno klasifikovať aj optimalizačné metódy.

1.1 Klasifikácia optimalizačných problémov

A. Spojitá optimalizácia

a) Úlohy s obmedzeniami

1. Lineárne programovanie

2. Nelineárne programovanie

3. Obmedzenia typu väzieb

4. Sieťové programovanie

5. Stochastické programovanie

b) Úlohy bez obmezení

1. Nelineárne rovnice

2. Nelineárne úlohy najmenších štvorcov

3. Globálnaoptimalizácia

4. Nediferenciálna optimalizácia

B. Nespojitá (diskrétna) optimalizácia

a) Celočíselné programovanie

b) Stochastické programovanie

1.2 Klasifikácia optimalizačných metód

A. Vyhľadávanie extrémov funkcií bez obmedzení

a) Analytické metódy riešenia voľného extrému

1. Jednorozmerové

2. Viacrozmerové

b) Iteračné metódy optimalizácie

1. Komparatívme

· S náhodným vyhľadávaním, genetické algoritmy

· S deterministickým vyhľadávaní

(Box-Wilsonova metóda, súradnicová komparácia, Gauss-Seidlova metóda)

2. S využitím prvej derivácie

(Regula falsi, gradientové metódy,...)

3. S využitím druhej derivácie

(Newtonova metóda,...)

B. Vyhľadávanie extrémov funkcií s obmedzeniami

a) Obmedzenia v tvare rovníc

1. Analytické metódy (Metóda Lagrangeových multiplikátorov)

2. Iteračné metódy

b) Obmedzenia v tvare nerovníc

1. Analytické metódy (Kuhn-Tuckerova metóda)

2. Penalizačné metódy

3. Iteračné metódy (Projekcia gradientu, metódy prípustných smerov,...)

C. Úlohy so špeciálnym tvarom účelovej funkcie a obmedzení

1. Lineárne programovanie (LP)

2. Celočíselné programovanie (IP)

3. Kvadratické programovanie (QP)

4. Geometrické programovanie (GP)

5. Dynamické programovanie (DP)

2 LINEÁRNE PROGRAMOVANIE (LP)

Lineárne programovanie je jednou oblasťou zo špeciálnych úloh matematického programovania. Väčšinou sú to úlohy ekonomického charakteru, problémy nutričného charakteru a pod. V lineárnom programovaní ide o úlohy viacparametrickej optimalizácie, keď účelová funkcia a jej ohraničenia sú lineárne. Všeobecne možno úlohy lineárneho programovania formulovať účelovou (objektívnou, kriteriálnou) funkciou v tvare:

max E(x) = c₁ x₁ + c₂ x₂ + ... + c_n x_n (1)

pri daných obmedzujúcich podmienkach:

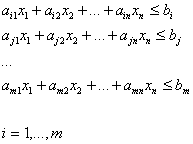(2)

(3)

a za podmienky nezápornosti:

, (4)

pričom

c_n – predstavujú cenové koeficienty

x_n – úrovne procesov alebo činností

a_mn – štruktúrne koeficienty

b_m – disponibilné faktory

E – hodnota kriteriálneho ukazovateľa.

Aby model mohol patriť do lineárneho programovania, musí úloha, problém vyhovovať určitým predpokladom proporcionality, nezápornosti, sčítateľnosti. Model lineárneho programovania vyžaduje metódu, ktorou sa dopracuje k riešeniu sústavy simultánnych rovníc.

2.1 Formulácia modelu LP

Metóda LP považuje úlohu za rozložiteľnú na rad elementárnych funkcií, na činnosti. Kvalita, množstvo každej činnosti sa nazýva úroveň alebo aj intenzita činnosti. Ak chceme zmeniť úroveň činnosti, musíme zmeniť vstupy a výstupy.

Predpoklady: 1. Proporcionalita (hypotéza lineárnosti) – v modeli LP kvantity rôznych tokov

sú vždy proporcionálne (úmerné) objemu činnosti.

Napr. ak chceme zdvojnásobiť objem činnosti, treba zdvojnásobiť všetky

toky vstupujúce do činnosti.

2. Nezápornosť – je možný ľubovoľný násobok činnosti, ale nie sú možné

záporné kvantity činnosti.

3. Sčítateľnosť – pre každú položku sa vyžaduje, aby sa celková špecifikovaná suma sústavy rovnala rozdielu sumy množstiev prúdiacich do rôznych činností a sumy vystupujúcich množstiev. Každá položka je vlastne rovnicou materiálovej bilancie.

2.2 Zostavenie modelu LP

Zostavenie modelu je hlavnou úlohou programovania. Treba systematizovať postupové kroky.

Matematický model úlohy je súbor matematických vzťahov, ktoré charakterizujú prípustné programy sústavy.

Prípustné programy sú tie, ktoré možno uskutočniť pri daných obmedzujúcich podmienkach sústavy.

1. Definovanie druhu činnosti: t.j. rozložiť celú úlohu na jednotlivé funkcie činnosti; zvoliť jednotku pre každú činnosť, pomocou ktorej možno merať jej kvantitu alebo úroveň (rozsah).

2. Definovať druh položky: t.j. určiť skupiny objektov, položky, ktoré sa potrebujú alebo vyrobia činnosťami; zvoliť jednotku každej položky.

3. Určiť koeficienty vstupu a výstupu: t.j. určiť množstvo každej spotrebovanej položky alebo položky vykonávaním každej činnosti pri jej jednotkovej úrovni. Tieto koeficienty vstupov a výstupov sú faktormi proporcionality medzi úrovňami, hladinami činností a tokmi položky.

4. Určiť exogénne (vonkajšie) toky: t.j. určiť čisté vstupy alebo výstupy položiek medzi sústavou ako celkom a okolím.

5. Určiť rovnicu materiálovej bilancie: t.j. priradiť nezáporné činnosti x₁, x₂,... všetkým činnostiam. Potom pre každú položku napísať rovnicu materiálovej bilancie, podľa ktorej algebraická suma tokov položky do každej činnosti (daná ako súčin úrovne činnosti násobenej príslušným koeficientom vstupu, výstupu) sa rovná exogénnemu toku položky.

2.3 Klasifikácia úloh lineárneho programovania

Charakteristickými vlastnosťami lineárneho programovania je linearita účelovej funkcie a linearita obmedzení. Prvú vlastnosť možno vyjadriť skalárnym súčinom

E(x₁, x₂, ...,x_n) = c^T.x (5)

druhá vlastnosť sa dá vyjadriť vzťahom

A.x £ b (6)

Uvedenými vzťahmi možno zapísať úlohy lineárneho programovania (primárny model).

Potom možno rozlíšiť štyri základné typy úloh:

a) max c^T.x A.x £ b (7)

b) min c^T.x A.x £ b

c) max c^T.x A.x ³ b

d) min c^T.x A.x ³ b

Tvary, ktoré sa líšia iba maximom či minimom účelovej funkcie (pri rovnakom otočení nerovností v obmedzeniach), sa upravia na rovnaký tvar zámenou min c^T.x za max (–c^T.x).

Ďalším variantom je úloha, ak niektoré obmedzenia musia byť splnené ako rovnosť. Úloha potom nadobúda tvar:

max E(x) = c^T.x (8)

pri obmedzeniach:

(9)

(10)

Posledným variantom je úloha, ak sú v obmedzeniach kombinované všetky tri tvary, teda:

(11)

(12)

(13)

2.4 Riešenie úloh lineárneho programovania

Uvažujme najprv úlohu v tvare (5), (6) pri podmienkach nezápornosti. Dimenzie polí nech sú:

(14)

V prvom kroku treba doplniť nerovnice (6) na rovnice tak, že ku každej nerovnici pridáme novú nezápornú premennú x_ij; Získa sa tým sústava lineárnych algebraických rovníc v tvare:

A.x = b (15)

kde

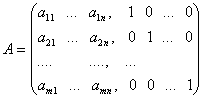(16)

nezákladné základné

premenné premenné

(17)

Sústava (16) reprezentuje m rovníc o m+n neznámych a je v tzv. kánonickom tvare. Základným riešením uvedenej sústavy je taká (m+n)-tica čísiel, kde hodnoty základných (bázických) premenných (priradených jednotkovej submatici) sú rovné hodnotám pravých strán. Základné riešenie má tvar:

(18)

Toto riešenie určite nemaximalizuje pravú stranu (má prvých n zložiek nulových). Postup, ktorý vyhľadáva optimum, je v nachádzaní rôznych základných riešení (15) tak, že sa bázické stĺpce v (16) postupne vymieňajú. Počet kombinácií týchto výmen je . Medzi týmito riešeniami je treba nájsť to, ktoré rovnicu (1) resp. (5) maximalizuje. Toto riešenie sa nazýva optimálne. Metóda získania všetkých základných riešení sa nazýva eliminačná. O riešení úloh lineárneho programovania platia dve dôležité vety .

Veta 1: Vektor x je základným riešením úlohy E(x₁, x₂, ...,x_n) = c^T.x (5), A.x £ b (6) práve vtedy, ak je aj krajným bodom množiny obmedzení A.x £ b (6).

Veta 2: (základná veta lineárneho programovania): Ak existuje optimálne riešenie úlohy lineárneho programovania, potom existuje aj základné riešenie tejto úlohy.

Z uvedených viet vyplýva, že optimálne riešenia sa nachádzajú iba na hranici konvexnej množiny obmedzení. Úloha lineárneho programovania má riešenie pre každý tvar (5), (6).

Bol vypracovaný efektívny postup, podľa ktorého sa postupuje k optimálnemu riešeniu v smere najväčšieho vzrastu účelovej funkcie a teda nie je potrebné analyzovať jednotlivo všetky základné riešenia pre danú funkciu. Postup je nazývaný ako metóda simplexovej tabuľky.

Zostavenie simplexovej tabuľky tkvie v zapísaní doplnenej sústavy rovníc (15) do tabuľky. Do posledného riadku sa zapíšu hodnoty účelovej funkcie s opačnými znamienkami podľa nasledovnej schémy:

x1	x2	....xn	xn+1	....xn+m
a11	a12	....a1n	1	....0	b1
...					...
am1	am2	.... amn	0	....1
-c1	-c2	....-cm	0	....0	f

Nové základné riešenie sa hľadá tak, že treba nájsť kľúčový riadok a kľúčový stĺpec. Ich priesečník udáva kľúčový prvok, ktorý sa v ďalšom kroku eliminuje ako bázický, a tak určuje ďalšie základné riešenie. Za kľúčový stĺpec sa vyberá ten, ktorý má v riadku účelovej funkcie záporné číslo s najväčšou absolútnou hodnotou. Za kľúčový riadok sa zasa vyberá ten, ktorého podiel pravej strany a kľúčového stĺpca je najmenší (vyberá sa len z nezáporných podielov).

2.5 Primárny a duálny model lineárneho programovania

K základnej úlohe lineárneho programovania (primárnemu modelu) existuje duálny tzv. združený model. Matematicky ide o nasledujúcu zámenu:

M={x³0, A.x£b, c^T.xmax} M^´={u³0, A^T.u£c, u^T.bmin} (19)

Primárny model Duálny model

Z definičných vzťahov (19) vyplýva, že duálna úloha k duálnej je opät primárna. Pre duálne úlohy v lineárnom programovaní platí základná veta o konečnej hodnote:

Ak má jeden zo združených matematických modelov riešenie s konečnou hodnotou účelovej funkcie potom má i druhý model optimálne riešenie s konečnou hodnotou účelovej funkcie a hodnoty účelových funkcií sú rovnaké. Ak však hodnota účelovej funkcie jedného zo združených matematických modelov môže rásť alebo klesať neobmedzene, potom druhý model nemá vôbec prípustné riešenie.

2.6 Kombinovaná úloha lineárneho programovania

Je posledným typom úlohy lineárneho programovania. Rieši sa použitím pomocných premenných – umelej bázy. Pri riešení sa postupuje nasledovne:

a) Obmedzenia typu rovnosť (=) sa doplnia pomocnými premennými s kladným znamienkom.

b) Obmedzenia typu nerovnosť (£) sa doplnia prídavnými premennými s kladným znamienkom na rovnice.

c) Obmedzenia typu nerovnosť sa doplnia prídavnými premennými so záporným znamienkom na rovnice. Do týchto rovníc sa dodajú ďalšie pomocné premenné ako v prípade obmedzenia rovnosťami (s kladnými znamienkami).

d) Zadefinuje sa dodatočná (pomocná) účelová funkcia ako súčet pomocných premenných z prípadu a) a c).

e) Potom sa rieši úloha postupom s umelou bázou.

3 VÝBER OPTIMALIZAČNEJ METÓDY

Je veľké množstvo optimalizačných úloh, ktoré možno riešiť pomocou rôznych súborov programov. Na pomerne jednoduché riešenie týchto problémov je vhodné prostredie MATLAB, nielen z hľadiska dostupnosti, ale aj preto, že práca s ním je súčasťou výučby.

3.1 Lineárne programovanie v prostredí MATLAB

MATLAB, ako účinný prostriedok, určený na prácu s vektormi a maticami robí tento súbor vyhovujúcim aj na riešenie typických problémov lineárneho programovania (LP). Zahŕňa výpočet základných prípustných riešení, extrémnych bodov a extrémnych smerov pri daných obmedzujúcich podmienkach, geometrické riešenie problémov LP, dvojfázovú metódou, duálny simplexový algoritmus, prírastok obmedzení a Gomoryho strihový stupňový algoritmus.

3.1.1 Funkcie MATLAB-u použité v súbore programov

Funkcia	Popis
abs	Absolútna hodnota
all	Pravdivá, ak všetky časti vektora sú nenulové
any	Pravdivá, ak žiadna časť vektora je nenulové
axis	Kontrola vyváženia osi a vzhľadu (prispôsobenia)
break	Ukončiť realizáciu slučky
clc	Vymazať príkazové okno
convhull	Konvexnosť
diff	Diferencia alebo približná derivácia
disp	Úprava displeja
eps	Pohyblivý bod relatívnej presnosti
eye	Identická matica
find	Nájde indexy nenulových prvkov
FontSize	Veľkosť písma
gea	Narába s určenou osou
get	Vlastnosti objektu
grid	Čiary mriežky
hold	Podrží aktuálny graf
inf	Nekonečno
intersect	Určí priesečník
isempty	Pravdivosť prázdnej matice
lenght	Dĺžka vektora
LineStyle	Druh čiary
LineWidht	Hrúbka čiary
max	Najväčšia zložka
min	Najmenšia zložka
msgbox	Schránka správ
nchoosek	Binomické koeficienty alebo všetky kombinácie
patch	Vytvorí cestu
pause	Čakanie na odpoveď uťžívateľa
plot	Lineárny graf
guestdlg	Dialógová schránka otázok
return	Návrat na dovolávanú funkciu
set	Nastavenie vlastností objektu
size	Veľkosť (rozmer) matice
sprintf	Zapíše formátované dáta do reťazcov
sqrt	Druhá odmocnina
stremp	Porovnanie prvkov
sum	Suma častí
title	Názov grafu
union	Zjednotenie množín
varargin	Zoznam premenných dĺžok vstupných argumentov
varargout	Zoznam premenných dĺžok výstupných argumentov
warning off	Zakáže všetky výstražné správy
xlabel	Označenie x-ovej osi
ylabel	Označenie y-ovej osi
zeros	Nulové zoskupenie

Poznámky

Symboly používané tomto dokumente:

· Rⁿ – n-dimenzionálny Euklidovský vektorový priestor. Každý člen tohto priestoru je n-dimenzionálny stĺpcový vektor.

· R ^{m x n} – množina všetkých reálnych matíc s m riadkami a n stĺpcami.

· T – operátor transpozície. V MATLAB-e sa používa aj operátor “ ' “ na vytvorenie transpozície reálneho vektora alebo reálnej matice.

· x^Ty – vnútorný súčin x a y.

· x ³ 0 – nezáporný vektor. Všetky zložky x sú väčšie alebo rovné nule.

3.1.2 Päť pomocných MATLAB-ovských funkcií

Tieto funkcie MATLAB-u sú určené na podporu pri riešení lineárnych optimalizačných problémov. Ich programy sú pomenované nasledovne: ver, delcols, MRT, MRTD a Br a mali by byť uložené v spoločnom adresári, kde sú uložené aj m-súbory na riešenie úloh lineárneho programovania.

function e = vr(m,i)

function d = delcols(d)

Prvé riadky programu v tele funkcie delcols sú zobrané zo súboru help v prostredí MATLAB. Dva vektory sú považované za vzájomné kópie (sa zhodujú), ak sa ich hodnoty nelíšia viac ako stonásobok stanovenej odchýlky. V MATLAB-e je toto číslo označené ako eps a je približne rovné

» format long

» eps

ans =

2.220446049250313e-016

» format short

» eps

ans =

2.2204e-016

Podľa potreby môžeme meniť predvolený formát zápisu desatinných miest short na long.

function [row, mi] = MRT(a, b)

function [m, j] = Br(d)

Kompletné programy uvedených funkcií sú uvedené v prílohe 1a až 1e.

3.1.3 Základné prípustné riešenia

Štandardná forma problémov lineárneho programovania býva vyjadrená nasledovne. Majme maticu A Î R^{m x n} a dva vektory c Î Rⁿ a b Î R^m, b ³ 0, treba nájsť vektor x Î Rⁿ , teda

min z = c^Tx

za predpokladu, že: Ax = b

x ³ 0

Funkcia vert = feassol(A, b) počíta všetky základné prípustné riešenia, ak existujú, v rámci zadaných obmedzení v štandardnej forme.

function vert = feassol(A, b)

(Príloha č.2)

Na ukážku funkčnosti tejto funkcie uvažujme nasledujúce obmedzujúce podmienky

x₁ + x₂ £ 6

x₂ £ 3

x₁, x₂ ³ 0

Na uvedenie systému  do štandardnej formy sú pridané 2 doplnkové premenné. Matica obmedzení A a pravá strana b majú potom tvar

» A=[1 1 1 0;0 1 0 1];

» b=[6;3];

» vert=feassol(A,b)

vert =

0 0 3 6

0 3 3 0

6 3 0 0

3 0 0 3

Na získanie hodnôt premenných x₁ a x₂ stačí vybrať riadky 1. a 2. z matice vert

» vert=vert(1:2, :)

vert =

0 0 3 6

0 3 3 0

3.1.4 Extrémne body a extrémne smery množiny obmedzení

Majme nasledovne formulovaný problém. Daná je polyédrická množina X = {x: Ax £ b or Ax³ b, x ³0}, v ktorej treba nájsť všetky extrémne body z X. Ak X je neohraničená, potom vyhľadávanie extrémnych bodov je bez závažných problémov. Ak úloha LP zahrňa súbor obmedzení v tvare rovnosti, potom ich možno pretransformovať pomocou dvojíc nerovnostných obmedzení. Toto je založené na nasledujúcich triviálnych vzťahoch: rovnosť a = b je ekvivalentná systému nerovností a £ b a a ³ b. Poznanie extrémnych bodov a extrémnych smerov polyédrickej množiny X je dôležité pre úplný matematický popis tejto množiny.

Extrémne body z množiny v zadaní môžu byť rátané použitím funkcie extrpts

function vert = extrpts(A, rel, b)

(Prílohač. 3a)

Uvažujme polyédrickú množinu X danú nerovnicami

-x₁ + x₂ £ 1

-0.1x₁ + x₂ £ 2

x₁, x₂ ³ 0

Na výpočet extrémnych bodov zadefinujeme

» A=[-1 1;-0.1 1];

» rel='<<';

» b=[1;2];

a riešime m-súborom extptrs

» vert=extrpts(A,rel,b)

vert =

0 0 1.1111

0 1.0000 2.1111

Extrémne body boli uložené stĺpcoch matice vert.

Extrémne smery, polyédrickej množiny X, ak existujú, možno vypočítať pomocou funkcie extrdir

function d = extrdir(A, rel, b)

(Prílohač. 3b)

Funkcia extrdir vráti prázdny operátor [ ] pre ohraničené polyédrické množiny.

Testujme funkciu použitím polyédrickej množiny, ktorá bola definovaná v poslednom príklade tejto časti.

Majme

» d = extrdir(A, rel, b)

d =

1.0000 0.9091

0 0.0909

3.1.5 Geometrické riešenie úloh lineárneho programovania

Riešenie problému LP s 2 premennými x₁ a x₂ môžeme hľadať geometricky v troch krokoch.

1. Zakreslí sa prípustná oblasť popísaná súborom obmedzení Ax £ b alebo Ax ³ b a x ³ 0.

2. Určí sa smer rovinnej plochy z = c₁x₁ + c₂x₂.

3. Pohybovaním rovinnej plochy možno nájsť vrchol (extrémny bod) z prípustnej oblasti, kde sa dosahuje minimálna alebo maximálna hodnota z alebo usúdime, že účelová funkcia je neohraničená.

Funkcia drawfr zahŕňa dva počiatočné kroky tejto metódy.

function drawfr(c, A, rel, b)

(Prílohač. 4)

Na otestovanie tejto funkcie uvažujme problém LP s piatimi obmedzeniami

» c=[-3 5];

» A=[-1 1;1 1;1 1;3 -1;1 -3];

» rel='<><<<';

» b=[1;1;5;7;1];

Graf z prípustnej oblasti a rovinnej plochy vyzerá nasledovne

» drawfr(c, A, rel, b)

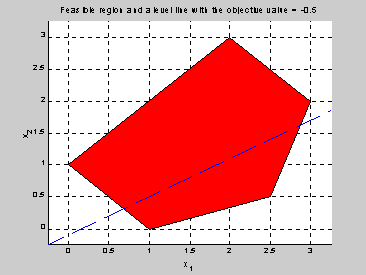
Pre minimalizáčný problém je optimálne riešenie nasledovné

x =

kým maximum účelovej funkcie je v bode

x =

Ďalší lineárny problém je definovaný nasledovne

» c=[1 1];

» A=[-1 1;-0.1 1];

» rel='<<';

» b=[1;2];

» drawfr(c, A, rel, b)

Extreme direction(s) of the constraint set

d =

1.0000 0.9091

0 0.0909

Extreme points of the constraint set

t =

0 0 1.1111

0 1.0000 2.1111

V tomto prípade sa graf  prípustnej oblasti nezobrazí. Extrémne smery a extrémne body sú mimo oblasti, preto sa objaví upozorňujúca správa.

3.1.6 Dvojfázová metóda

Dvojfázová metóda je jedným zo základných výpočtových prostriedkov používaných v  LP. Princíp tejto metódy uvedený v tejto časti ukazuje všetky jej prednosti. Problém lineárneho programovania môže byť riešený buď ako minimalizačný alebo maximalizačný problém. Optimálne riešenie je vyhľadávané v polyédrickej množine, ktorá je popísaná pomocou nerovností a/alebo obmedzení typu rovnosti spolu s nezápornými obmedzeniami uloženými na premenné.

Funkcia simplex2p zobrazuje správy o riešenom lineárnom probléme. Tieto zahŕňajú:

· informáciu o jednoznačnosti optimálneho riešenia

· informáciu o neohraničenosti účelovej funkcie (ak existuje)

· informáciu o tom, či je prípustná oblasť prázdna.

Na doplnenie uvedených prostriedkov sú zabudované mechanizmy umožňujúce riešiť lineárne problémy so sústavami zahŕňajúce redundantné obmedzenia. Taktiež zahŕňa Blandovo pravidlo zabraňujúce zacyklovaniu problému.

Počas práce s funkciou simplex2p užívateľ má možnosť sledovať kroky výpočtu (použitím tlačidla Yes v okne správy).

function simplex2p(type, c, A, rel, b)

(Prílohač. 5a)

MATLAB-ovská subfunkcia loop je zahrnutá v m-súbore simplex2p. Je v ňom zabudovaná hlavná slučka simplexového algoritmu.

Otestujeme túto funkciu na 4 lineárnych problémoch.

Nech

» type='min';

» c=[-3 4];

» A=[1 1;2 3];

» rel='<>';

» b=[4;18];

Jednoducho možno úlohu skontrolovať bud nakreslením grafu množiny obmedzení alebo priebehom funkcie drawfr na zadaných údajoch.

» simplex2p(type, c, A, rel, b)

Initial tableau

A =

1 1 1 0 1 0 4

2 3 0 -1 0 1 18

-3 4 0 0 0 0 0

-3 -4 -1 1 0 0 -22

Press any key to continue ...

pivot row-> 1 pivot column-> 1

Tableau 1

A =

1 1 1 0 1 0 4

0 1 -2 -1 -2 1 10

0 7 3 0 3 0 12

0 -1 2 1 3 0 -10

Press any key to continue ...

pivot row-> 1 pivot column-> 2

Tableau 2

A =

1 1 1 0 1 0 4

-1 0 -3 -1 -3 1 6

-7 0 -4 0 -4 0 -16

1 0 3 1 4 0 -6

Press any key to continue ...

End of Phase 1

*********************************

Empty feasible region

Ďalšia úloha LP má neohraničenú účelovú funkciu. Nech

» type = 'max';

» c = [3 2 1];

» A =[2 -3 2;-1 1 1];

» rel='<<';

» b=[3;55];

Pomocou funkcie simplex2p získame

» simplex2p(type, c, A, rel, b)

Initial tableau

A =

2 -3 2 1 0 3

-1 1 1 0 1 55

-3 -2 -1 0 0 0

Press any key to continue ...

pivot row-> 1 pivot column-> 1

Tableau 1

A =

1.0000 -1.5000 1.0000 0.5000 0 1.5000

0 -0.5000 2.0000 0.5000 1.0000 56.5000

0 -6.5000 2.0000 1.5000 0 4.5000

Press any key to continue ...

Unbounded optimal solution with z= Inf

End of Phase 1

*********************************

V nasledujúcej úlohe sa budeme zaoberať lineárnym problémom, ktorý je opísaný sústavou dvoch rovníc so siedmymi premennými

» type = 'min';

» c = [3 4 6 7 1 0 0];

» A = [2 -1 1 6 -5 -1 0;1 1 2 1 2 0 -1];

» b = [6;3];

» simplex2p(type, c, A, rel, b)

Initial tableau

A =

2 -1 1 6 -5 -1 0 1 0 6

1 1 2 1 2 0 -1 0 1 3

3 4 6 7 1 0 0 0 0 0

-3 0 -3 -7 3 1 1 0 0 -9

Press any key to continue ...

pivot row-> 1 pivot column-> 1

Tableau 1

A =

Columns 1 through 7

1.0000 -0.5000 0.5000 3.0000 -2.5000 -0.5000 0

0 1.5000 1.5000 -2.0000 4.5000 0.5000 -1.0000

0 5.5000 4.5000 -2.0000 8.5000 1.5000 0

0 -1.5000 -1.5000 2.0000 -4.5000 -0.5000 1.0000

Columns 8 through 10

0.5000 0 3.0000

-0.5000 1.0000 0

-1.5000 0 -9.0000

1.5000 0 0

Press any key to continue ...

pivot row-> 2 pivot column-> 2

Tableau 2

A =

Columns 1 through 7

1.0000 0 1.0000 2.3333 -1.0000 -0.3333 -0.3333

0 1.0000 1.0000 -1.3333 3.0000 0.3333 -0.6667

0 0 -1.0000 5.3333 -8.0000 -0.3333 3.6667

0 0 0 0 0 0 0

Columns 8 through 10

0.3333 0.3333 3.0000

-0.3333 0.6667 0

0.3333 -3.6667 -9.0000

1.0000 1.0000 0

Press any key to continue ...

End of Phase 1

*********************************

Tableau 1

A =

Columns 1 through 7

1.0000 0 1.0000 2.3333 -1.0000 -0.3333 -0.3333

0 1.0000 1.0000 -1.3333 3.0000 0.3333 -0.6667

0 0 -1.0000 5.3333 -8.0000 -0.3333 3.6667

Column 8

3.0000

0

-9.0000

Press any key to continue ...

pivot row-> 2 pivot column-> 3

Tableau 2

A =

Columns 1 through 7

1.0000 -1.0000 0 3.6667 -4.0000 -0.6667 0.3333

0 1.0000 1.0000 -1.3333 3.0000 0.3333 -0.6667

0 1.0000 0 4.0000 -5.0000 0.0000 3.0000

Column 8

3.0000

0

-9.0000

Press any key to continue ...

pivot row-> 2 pivot column-> 5

Tableau 3

A =

Columns 1 through 7

1.0000 0.3333 1.3333 1.8889 0 -0.2222 -0.5556

0 0.3333 0.3333 -0.4444 1.0000 0.1111 -0.2222

0 2.6667 1.6667 1.7778 0 0.5556 1.8889

Column 8

3.0000

0

-9.0000

Press any key to continue ...

End of Phase 2

*********************************

Problem has a finite optimal solution

Values of the legitimate variables:

x(1)= 3.000000

x(2)= 0.000000

x(3)= 0.000000

x(4)= 0.000000

x(5)= 0.000000

x(6)= 0.000000

x(7)= 0.000000

Objective value at the optimal point:

z= 9.000000

Ak je lineárna úloha degenerovaná, potom je možné, že táto metóda nebude ukončená. Aby sme sa vyhli zacyklovaniu využije sa Blandovo pravidlo zahrnuté vo funkcii loop (Príloha č. 5b). Úloha je nasledovná

type = 'min';

c = [-3/4 150 –1/50 6];

A = [1/4 –60 –1/25 9; 1/2 -90 –1/50 3; 0 0 1 0];

rel = '<<<';

b = [0 0 1];

Funkcia simplex2p vytvorí nasledujúce tabuľky

simplex2p(type, c, A, rel, b)

Initial tableau

A =

Columns 1 through 7

0.2500 -60.0000 -0.0400 9.0000 1.0000 0 0

0.5000 -90.0000 -0.0200 3.0000 0 1.0000 0

0 0 1.0000 0 0 0 1.0000

-0.7500 150.0000 -0.0200 6.0000 0 0 0

Column 8

0

0

1.0000

0

Press any key to continue ...

pivot row-> 1 pivot column-> 1

Tableau 1

A =

Columns 1 through 7

1.0000 -240.0000 -0.1600 36.0000 4.0000 0 0

0 30.0000 0.0600 -15.0000 -2.0000 1.0000 0

0 0 1.0000 0 0 0 1.0000

0 -30.0000 -0.1400 33.0000 3.0000 0 0

Column 8

0

0

1.0000

0

Press any key to continue ...

pivot row-> 2 pivot column-> 2

Tableau 2

A =

Columns 1 through 7

1.0000 0 0.3200 -84.0000 -12.0000 8.0000 0

0 1.0000 0.0020 -0.5000 -0.0667 0.0333 0

0 0 1.0000 0 0 0 1.0000

0 0 -0.0800 18.0000 1.0000 1.0000 0

Column 8

0

0

1.0000

0

Press any key to continue ...

pivot row-> 1 pivot column-> 3

Tableau 3

A =

Columns 1 through 7

3.1250 0 1.0000 -262.5000 -37.5000 25.0000 0

-0.0063 1.0000 0 0.0250 0.0083 -0.0167 0

-3.1250 0 0 262.5000 37.5000 -25.0000 1.0000

0.2500 0 0 -3.0000 -2.0000 3.0000 0

Column 8

0

0

1.0000

0

Press any key to continue ...

pivot row-> 2 pivot column-> 4

Tableau 4

A =

1.0e+004 *

Columns 1 through 7

-0.0062 1.0500 0.0001 0 0.0050 -0.0150 0

-0.0000 0.0040 0 0.0001 0.0000 -0.0001 0

0.0062 -1.0500 0 0 -0.0050 0.0150 0.0001

-0.0000 0.0120 0 0 -0.0001 0.0001 0

Column 8

0

0

0.0001

0

Press any key to continue ...

pivot row-> 3 pivot column-> 1

Tableau 5

A =

Columns 1 through 7

0 0 1.0000 0 0 0 1.0000

0 -2.0000 0 1.0000 0.1333 -0.0667 0.0040

1.0000 -168.0000 0 0 -0.8000 2.4000 0.0160

0 36.0000 0 0 -1.4000 2.2000 0.0080

Column 8

1.0000

0.0040

0.0160

0.0080

Press any key to continue ...

pivot row-> 2 pivot column-> 5

Tableau 6

A =

Columns 1 through 7

0 0 1.0000 0 0 0 1.0000

0 -15.0000 0 7.5000 1.0000 -0.5000 0.0300

1.0000 -180.0000 0 6.0000 0 2.0000 0.0400

0 15.0000 0 10.5000 0 1.5000 0.0500

Column 8

1.0000

0.0300

0.0400

0.0500

Press any key to continue ...

End of Phase 1

*********************************

Problem has a finite optimal solution

Values of the legitimate variables:

x(1)= 0.040000

x(2)= 0.000000

x(3)= 1.000000

x(4)= 0.000000

Objective value at the optimal point:

z= -0.050000

Posledný vstup v stĺpci 8, v tabuľke 1 až 4, je rovný nule. Treba pripomenúť, že toto je aktuálna hodnota účelovej funkcie. Simplexový algoritmus skúša zlepšiť aktuálne základné prípustné riešenia a po niekoľkých pokusoch sa mu to podarí. Dve základné premenné v tabuľke 1 až 4 sú obe rovné nule. Na základe týchto poznatkov možno povedať, že daný problém je degenerovaný. Bez zabudovaného mechanizmu, ktorý by zabraňoval zacyklovaniu, tento algoritmus nemôže skončiť.

3.1.7 Duálny simplexový algoritmus

Iná metóda, ktorá je veľmi zaujímavá v LP, sa nazýva Duálny simplexový algoritmus. Optimalizačný problém, ktorý môže byť riešený pomocou tejto metódy je formulovaný takto

min (max) z = c^Tx

za predpokladu, že: Ax ³ b

x ³ 0

Zložky vektora b nevyžadujú splnenie podmienky nezápornosti obmedzení. Duálny simplexový algoritmus má veľké možnosti aplikácie pre dalšie úlohy LP. Je použiteľný napríklad v rámci  Gomoryho strihových algoritmov na riešenie problémov celočíselného programovania.

Funkcia dsimplex vypočíta optimálne riešenie optimalizačného problému, ktorý je definovaný vyššie. Jedna z elegantných možností tejto metódy je schopnosť zistiť prípad prázdnej prípustnej oblasti. Funkcia, o ktorej hovoríme, umožňuje voliť štyri vstupné parametre types, c, A a b.

function varargout = dsimplex(type, c, A, b)

(Prílohač. 6)

Funkcia dsimplex dovoľuje rôzny počet výstupných parametrov. Indexy základných premenných sa vždy zobrazia v konečnej tabuľke. Konečnú tabuľku taktiež možno uložiť vo vhodnej forme . Napríklad, realizácia nasledovného príkazu [subs, B]=dsimplex(type, c, A, b) vráti, okrem iného, indexy základných premenných uložené v premennej subs a konečnú tabuľku v premennej B.

Nech

type = 'min';

c = [-2 3 4];

A = [-1 –1 –1;2 2 2];

b = [-1;4];

Jednoducho možno skontrolovať, či systém obmedzení definuje prázdnu množinu. Využitím funkcie dsimplex získame

subs = dsimplex(type, c, A, b)

Initial tableau

A =

1 1 1 1 0 1

-2 -2 -2 0 1 -4

-2 3 4 0 0 0

Press any key to continue ...

pivot row-> 2 pivot column-> 1

Tableau 1

A =

0 0 0 1.0000 0.5000 -1.0000

1.0000 1.0000 1.0000 0 -0.5000 2.0000

0 5.0000 6.0000 0 -1.0000 4.0000

Press any key to continue ...

Empty feasible region

subs =

4

1

V tomto príklade použijeme funkciu dsimplex na hľadanie optimálneho riešenia problému so štyrmi premennými a tromi obmedzeniami.

type = 'max';

c = [1 2 3 –1];

A = [2 1 5 0;1 2 3 0;1 1 1 1];

b = [20;25;10];

subs = dsimplex(type, c, A, b)

Initial tableau

A =

-2 -1 -5 0 1 0 0 -20

-1 -2 -3 0 0 1 0 -25

-1 -1 -1 -1 0 0 1 -10

-1 -2 -3 1 0 0 0 0

Press any key to continue ...

pivot row-> 1 pivot column-> 2

Tableau 1

A =

2 1 5 0 -1 0 0 20

3 0 7 0 -2 1 0 15

1 0 4 -1 -1 0 1 10

3 0 7 1 -2 0 0 40

Press any key to continue ...

Problem has a finite optimal solution

Values of the legitimate variables:

x(1)= 0.000000

x(2)= 20.000000

x(3)= 0.000000

x(4)= 0.000000

Objective value at the optimal point:

z= 40.000000

Indices of basic variables in the final tableau:

subs =

2

6

7

3.1.8 Pridanie obmedzení

Pridanie obmedzení môže byť zaujímavé hlavne z hľadiska citlivostnej analýzy. Predpokladajme, že problém LP bol riešený použitím jednej z metód, o ktorých sme už hovorili. Predpokladajme, že je daná konečná tabuľka A a vektor subs – vektor indexov základných premenných. Chceme nájsť optimálne riešenie pôvodného problému pridaním ďalších obmedzení a^Tx £ d alebo a^Tx ³ d.

Možno ho riešiť funkciou addconstr(type, A, subs, a, rel, d)

function addconstr(type, A, subs, a, rel, d)

(Prílohač. 7)

Riešme nasledujúcu úlohu

type = 'max';

A = [-2 0 5 1 2 –1 6; 11 1 –18 0 –7 4 4; 3 0 2 0 2 1 106];

subs = [4; 2];

a = [4 1 0 4];

rel = '>';

d = 29;

addconstr(type, A, subs, a, rel, d)

Initial tableau

A =

-2 0 5 1 2 -1 0 6

11 1 -18 0 -7 4 0 4

-1 0 2 0 1 0 1 -1

3 0 2 0 2 1 0 106

Press any key to continue ...

pivot row-> 3 pivot column-> 1

Tableau 1

A =

0 0 1 1 0 -1 -2 8

0 1 4 0 4 4 11 -7

1 0 -2 0 -1 0 -1 1

0 0 8 0 5 1 3 103

Press any key to continue ...

Empty feasible region

Zmenou pridaného obmedzenia 3x₁ + x₂ + 3x₄ £ 20, získame

a = [3 1 0 3];

rel = '<';

d = 20;

addconstr(type, A, subs, a, rel, d)

Initial tableau

A =

-2 0 5 1 2 -1 0 6

11 1 -18 0 -7 4 0 4

-2 0 3 0 1 -1 1 -2

3 0 2 0 2 1 0 106

Press any key to continue ...

pivot row-> 3 pivot column-> 6

Tableau 1

A =

0 0 2 1 1 0 -1 8

3 1 -6 0 -3 0 4 -4

2 0 -3 0 -1 1 -1 2

1 0 5 0 3 0 1 104

Press any key to continue ...

pivot row-> 2 pivot column-> 3

Tableau 2

A =

Columns 1 through 7

1.0000 0.3333 0 1.0000 0 0 0.3333

-0.5000 -0.1667 1.0000 0 0.5000 0 -0.6667

0.5000 -0.5000 0 0 0.5000 1.0000 -3.0000

3.5000 0.8333 0 0 0.5000 0 4.3333

Column 8

6.6667

0.6667

4.0000

100.6667

Press any key to continue ...

Problem has a finite optimal solution

Values of the legitimate variables:

x(1)= 0.000000

x(2)= 0.000000

x(3)= 0.666667

x(4)= 6.666667

x(5)= 0.000000

x(6)= 4.000000

x(7)= 0.000000

Objective value at the optimal point:

z= 100.666667

3.1.9 Gomoryho strihový algoritmus

Niektoré problémy, vyskytujúce sa v ekonomike možno formulovať ako lineárne problémy s  premennými, ktorým sú striktne priradené celočíselné hodnoty

min(max) z = c*x

Za predpokladu, že: Ax £ b

x ³ 0 a celočíselné

kde vektor pravých strán b je nezáporný. Jedným spomedzi numerických algoritmov navrhnutých na riešenie takýchto úloh je Gomoryho algoritmus, nazývaný aj ako strihový algoritmus. V tejto časti je tento nástroj uložený pod funkciou cpa.

function cpa(type, c, A, b)

(Prílohač. 8a)

Subfunkcia fractp (Prílohač. 8b) je volaná z vnútra funkcie cpa. Počíta zlomkové časti reálnych čísel , ktoré sú uložené v matici. Funkcia cpa môže vyvolať aj dalšiu funkciu simplex. Nakoniec nájde riešenie problému formulovaného na žačiatku tejto časti bez uplatnenia reštrikcie na celočíselnosť premenných.

function[A, subs, x, z] = simplex(type, c, A, b, varargin);

(Prílohač. 8c)

Otestujme funkciu cpa na dvoch problémoch.

Nech

type = 'min';

c = [1 –3];

A = [1 –1;2 4];

b = [2;15];

Využitím možnosti sledovania výpočtu, budú zobrazené nasledovné tabuľky

cpa(type, c, A, b)

________________________________________________

Tableaux of the Simplex Algorithm

________________________________________________

Initial tableau

A =

1 -1 1 0 2

2 4 0 1 15

1 -3 0 0 0

Press any key to continue ...

Final tableau

A =

1.5000 0 1.0000 0.2500 5.7500

0.5000 1.0000 0 0.2500 3.7500

2.5000 0 0 0.7500 11.2500

Press any key to continue ...

________________________________________________

Tableaux of the Dual Simplex Method

________________________________________________

pivot row-> 3 pivot column-> 4

Tableau 1

A =

1.5000 0 1.0000 0.2500 0 5.7500

0.5000 1.0000 0 0.2500 0 3.7500

-0.5000 0 0 -0.2500 1.0000 -0.7500

2.5000 0 0 0.7500 0 11.2500

Press any key to continue ...

Final tableau

A =

1 0 1 0 1 5

0 1 0 0 1 3

2 0 0 1 -4 3

1 0 0 0 3 9

Press any key to continue ...

Problem has a finite optimal solution

Values of the legitimate variables:

x(1)= 0

x(2)= 3

Objective value at the optimal point:

z= -9.000000

Zobrazí sa len počiatočná a konečná tabuľka simplexového algoritmu. Avšak, všetky tabuľky vytvorené počas realizácie duálneho simplexového algoritmu sú tam zahrnuté.

Nech teraz

type = 'min';

c = [1 –2];

A = [2 1;-4 4];

b = [5;5];

cpa(type, c, A, b)

________________________________________________

Tableaux of the Simplex Algorithm

________________________________________________

Initial tableau

A =

2 1 1 0 5

-4 4 0 1 5

1 -2 0 0 0

Press any key to continue ...

Final tableau

A =

1.0000 0 0.3333 -0.0833 1.2500

0 1.0000 0.3333 0.1667 2.5000

0 0 0.3333 0.4167 3.7500

Press any key to continue ...

________________________________________________

Tableaux of the Dual Simplex Method

________________________________________________

pivot row-> 3 pivot column-> 3

Tableau 1

A =

1.0000 0 0.3333 -0.0833 0 1.2500

0 1.0000 0.3333 0.1667 0 2.5000

0 0 -0.3333 -0.1667 1.0000 -0.5000

0 0 0.3333 0.4167 0 3.7500

Press any key to continue ...

pivot row-> 4 pivot column-> 4

Tableau 2

A =

1.0000 0 0 -0.2500 1.0000 0 0.7500

0 1.0000 0 0 1.0000 0 2.0000

0 0 1.0000 0.5000 -3.0000 0 1.5000

0 0 0 -0.7500 0 1.0000 -0.7500

0 0 0 0.2500 1.0000 0 3.2500

Press any key to continue ...

Final tableau

A =

1.0000 0 0 0 1.0000 -0.3333 1.0000

0 1.0000 0 0 1.0000 0 2.0000

0 0 1.0000 0 -3.0000 0.6667 1.0000

0 0 0 1.0000 0 -1.3333 1.0000

0 0 0 0 1.0000 0.3333 3.0000

Press any key to continue ...

Problem has a finite optimal solution

Values of the legitimate variables:

x(1)= 1

x(2)= 2

Objective value at the optimal point:

z= -3.000000

Funkcia cpa bola rozsiahle testovaná. Zlyhala však pri výpočte optimálneho riešenia nasledujúceho problému celočíselného programovania.

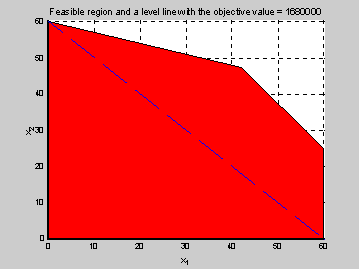
max z = 3x₁ + 13x₂

za predpokladu, že: 2x₁ + 9x₂ £ 40

11x₁ – 8x₂ £ 82

x₁, x₂ ³ 0 a celočíselné

4 TESTOVANÉ PRÍKLADY

Výpočet základných prípustných riešení

Funkcia vert = feassol(A, b)

» A=[1.5 0 2 2.5 1 1;2 1.5 2 0 1 0;-1 0.5 0 1 0 1;0 -1 0.5 2 0 1]

» b=[1200;1400;0;0]

» vert = feassol(A, b)

Na uvedenie systému  do štandardnej formy sú pridané 2 doplnkové premenné.

vert =

57.1429 240.0000 266.6667

114.2857 160.0000 266.6667

228.5714 0 0

0 0 133.3333

657.1429 680.0000 466.6667

0 160.0000 0

Na získanie hodnôt premenných x₁ a x₂ stačí vybrať riadky 1. a 2. z matice vert

» vert=vert(1:2, :)

vert =

57.1429 240.0000 266.6667

114.2857 160.0000 266.6667

Extrémne body z množiny v zadaní môžu byť rátané použitím funkcie extrpts

» A=[1.5 0 2 2.5;2 1.5 2 0;-1 0.5 0 1;0 -1 0.5 2]

» rel='<<<<'

» b=[1200;1400;0;0]

» » vert=extrpts(A,rel,b)

vert =

0 107.6923 280.0000 400.0000 700.0000

0 215.3846 560.0000 400.0000 0

0 430.7692 0 0 0

0 0 0 200.0000 0

Dvojfázová metóda

Chemický závod vyrába 4 výrobky: V₁, V₂, V₃, V₄. Pri zostavovaní výrobného programu je treba počítať s obmedzenou kapacitou zariadenia Z (je v dispozícii 1200 hod. štvrťročne) a s obmedzeným množstvom suroviny S (1400 t na štvrťroka). Výrobky V₁ a V₂ sú polotovary potrebné na výrobu výrobkov V₂, V₃ a V₄ môžu však byť tiež predávané. Ceny výrobkov sú: 300 Sk za 1 t V₁, 600 Sk za 1 t V₂, 1000 Sk za 1 t V₃ a 3000 Sk za 1 t V₄. Je treba stanoviť taký výrobný program závodu, aby odbyt závodu bol maximálny.

» type='max'

» c=[300 450 700 1500]

» A=[1.5 0 2 2.5;2 1.5 2 0;-1 0.5 0 1;0 -1 0.5 2]

» rel='<<<<'

» b=[1200;1400;0;0]

» simplex2p(type, c, A, rel, b)

Initial tableau

A =

1.0e+003 *

Columns 1 through 7

0.0015 0 0.0020 0.0025 0.0010 0 0

0.0020 0.0015 0.0020 0 0 0.0010 0

-0.0010 0.0005 0 0.0010 0 0 0.0010

0 -0.0010 0.0005 0.0020 0 0 0

-0.3000 -0.4500 -0.7000 -1.5000 0 0 0

Columns 8 through 9

0 1.2000

0 1.4000

0 0

0.0010 0

0 0

Press any key to continue ...

pivot row-> 2 pivot column-> 1

Tableau 1

A =

1.0e+005 *

Columns 1 through 7

0 -0.0000 0.0000 0.0000 0.0000 -0.0000 0

0.0000 0.0000 0.0000 0 0 0.0000 0

0 0.0000 0.0000 0.0000 0 0.0000 0.0000

0 -0.0000 0.0000 0.0000 0 0 0

0 -0.0022 -0.0040 -0.0150 0 0.0015 0

Columns 8 through 9

0 0.0015

0 0.0070

0 0.0070

0.0000 0

0 2.1000

Press any key to continue ...

pivot row-> 3 pivot column-> 2

Tableau 2

A =

1.0e+005 *

Columns 1 through 7

0 0 0.0000 0.0000 0.0000 -0.0000 0.0000

0.0000 0 0.0000 -0.0000 0 0.0000 -0.0000

0 0.0000 0.0000 0.0000 0 0.0000 0.0000

0 0 0.0000 0.0000 0 0.0000 0.0000

0 0 -0.0022 -0.0132 0 0.0024 0.0018

Columns 8 through 9

0 0.0078

0 0.0028

0 0.0056

0.0000 0.0056

0 3.3600

Press any key to continue ...

pivot row-> 4 pivot column-> 3

Tableau 3

A =

1.0e+005 *

Columns 1 through 7

0 0 0 0.0000 0.0000 -0.0000 0.0000

0.0000 0 0 -0.0000 0 0.0000 -0.0000

0 0.0000 0 -0.0000 0 0.0000 0.0000

0 0 0.0000 0.0000 0 0.0000 0.0000

0 0 0 -0.0085 0 0.0031 0.0032

Columns 8 through 9

-0.0000 0.0018

-0.0000 0.0011

-0.0000 0.0022

0.0000 0.0043

0.0017 4.3077

Press any key to continue ...

pivot row-> 4 pivot column-> 4

Tableau 4

A =

1.0e+005 *

Columns 1 through 7

0 0 -0.0000 0 0.0000 -0.0000 -0.0000

0.0000 0 0.0000 0 0 0.0000 -0.0000

0 0.0000 0.0000 0 0 0.0000 0.0000

0 0 0.0000 0.0000 0 0.0000 0.0000

0 0 0.0039 0 0 0.0043 0.0056

Columns 8 through 9

-0.0000 0.0010

0.0000 0.0040

-0.0000 0.0040

0.0000 0.0020

0.0047 6.0000

Press any key to continue ...

End of Phase 1

*********************************

Problem has a finite optimal solution

Values of the legitimate variables:

x(1)= 400.000000

x(2)= 400.000000

x(3)= 0.000000

x(4)= 200.000000

Objective value at the optimal point:

z= 600000.000000

Geometrické riešenie

Stanovte výrobný program podniku vyrábajúceho 2 typy zameniteľných výrobkov za týchto podmienok:

Kapacita zlievarne podniku môže vyrobiť odliatky najviac pre 80 kusov typu I alebo 100 kusov typu II. Kapacita lisovne môže vyrobiť výlisky najviac pre 200 kusov typu I alebo pre 60 kusov typu II. Montzáž typu I má kapacitu 60 kusov a montáž typu II 80 kusov. Cena 1 kusu oboch typov je 2800 SK. Výrobný program má zaistiť maximálnu hodnotu produkcie.

» c=[28000 28000]

» A=[1 0;0 1;1/80 1/100;1/200 1/60;1 0;0 1]

» rel='>><<<<'

» b=[0;0;1;1;60;80]

» drawfr(c, A, rel, b)

Graf z prípustnej oblasti

Duálny simplexový algoritmus

Čokoládovňa vyrába 5 druhov výrobkov. Spotrebúva 3 základné suroviny: tuk, kakao a cukor, ktoré sú v dispozícii v obmedzených množstvách: 1500 kg, 300 kg a 450 kg na deň. Kapacita strojového zariadenia je dostatočná, rovnako ako energia a pracovné sily; ďalšie zdroje sú v dispozícii v dostatočnom množstve. Odbytové ceny výrobkov v Sk/1 kg sú: V₁=20 Sk, V₂=120 Sk, V₃=100 Sk, V₄=140 Sk, V₅=40 Sk. Stanovte denný program tak, aby hodnota výroby v Sk bola maximálna.

» type='max'

» c=[20 120 100 140 40]

» A=[0 0.4 0.3 0.6 0.6;0.05 0.2 0.1 0.1 0;0.1 0.2 0.2 0.1 0.2]

» b=[1500;300;450]

» subs = dsimplex(type, c, A, b)

Initial tableau

A =

1.0e+003 *

Columns 1 through 7

0 -0.0004 -0.0003 -0.0006 -0.0006 0.0010 0

-0.0001 -0.0002 -0.0001 -0.0001 0 0 0.0010

-0.0001 -0.0002 -0.0002 -0.0001 -0.0002 0 0

-0.0200 -0.1200 -0.1000 -0.1400 -0.0400 0 0

Columns 8 through 9

0 -1.5000

0 -0.3000

0.0010 -0.4500

0 0

Press any key to continue ...

pivot row-> 1 pivot column-> 3

Tableau 1

A =

1.0e+005 *

Columns 1 through 7

0 0.0000 0.0000 0.0000 0.0000 -0.0000 0

-0.0000 -0.0000 0 0.0000 0.0000 -0.0000 0.0000

-0.0000 0.0000 0 0.0000 0.0000 -0.0000 0

-0.0002 0.0001 0 0.0006 0.0016 -0.0033 0

Columns 8 through 9

0 0.0500

0 0.0020

0.0000 0.0055

0 5.0000

Press any key to continue ...

Problem has a finite optimal solution

Values of the legitimate variables:

x(1)= 0.000000

x(2)= 0.000000

x(3)= 5000.000000

x(4)= 0.000000

x(5)= 0.000000

Objective value at the optimal point:

z= 500000.000000

Indices of basic variables in the final tableau:

subs =

3

7

8

» type='max'

» c=[20 120 100 140 40]

» A=[0 0.4 0.3 0.6 0.6;0.05 0.2 0.1 0.1 0;0.1 0.2 0.2 0.1 0.2]

» rel='<<<'

» b=[1500;300;450]

» simplex2p(type, c, A, rel, b)

Initial tableau

A =

1.0e+003 *

Columns 1 through 7

0 0.0004 0.0003 0.0006 0.0006 0.0010 0

0.0001 0.0002 0.0001 0.0001 0 0 0.0010

0.0001 0.0002 0.0002 0.0001 0.0002 0 0

-0.0200 -0.1200 -0.1000 -0.1400 -0.0400 0 0

Columns 8 through 9

0 1.5000

0 0.3000

0.0010 0.4500

0 0

Press any key to continue ...

pivot row-> 3 pivot column-> 1

Tableau 1

A =

1.0e+004 *

Columns 1 through 7

0 0.0000 0.0000 0.0001 0.0001 0.0001 0

0 0.0000 0 0.0000 -0.0000 0 0.0001

0.0001 0.0002 0.0002 0.0001 0.0002 0 0

0 -0.0080 -0.0060 -0.0120 0 0 0

Columns 8 through 9

0 0.1500

-0.0001 0.0075

0.0010 0.4500

0.0200 9.0000

Press any key to continue ...

pivot row-> 2 pivot column-> 2

Tableau 2

A =

1.0e+005 *

Columns 1 through 7

0 0 0.0000 0.0000 0.0000 0.0000 -0.0000

0 0.0000 0 0.0000 -0.0000 0 0.0001

0.0000 0 0.0000 0 0.0000 0 -0.0002

0 0 -0.0006 -0.0008 -0.0008 0 0.0080

Columns 8 through 9

0.0000 0.0120

-0.0001 0.0075

0.0002 0.0300

-0.0020 1.5000

Press any key to continue ...

pivot row-> 3 pivot column-> 3

Tableau 3

A =

1.0e+005 *

Columns 1 through 7

-0.0000 0 0 0.0000 0.0000 0.0000 -0.0000

0 0.0000 0 0.0000 -0.0000 0 0.0001

0.0000 0 0.0000 0 0.0000 0 -0.0001

0.0003 0 0 -0.0008 0.0004 0 0.0020

Columns 8 through 9

-0.0000 0.0075

-0.0001 0.0075

0.0001 0.0150

0.0040 2.4000

Press any key to continue ...

pivot row-> 2 pivot column-> 4

Tableau 4

A =

1.0e+005 *

Columns 1 through 7

-0.0000 -0.0000 0 0 0.0000 0.0000 -0.0001

0 0.0000 0 0.0000 -0.0000 0 0.0002

0.0000 0 0.0000 0 0.0000 0 -0.0001

0.0003 0.0016 0 0 -0.0012 0 0.0180

Columns 8 through 9

0.0000 0.0015

-0.0001 0.0150

0.0001 0.0150

-0.0040 3.6000

Press any key to continue ...

pivot row-> 1 pivot column-> 5

Tableau 5

A =

1.0e+005 *

Columns 1 through 7

-0.0000 -0.0000 0 0 0.0000 0.0000 -0.0001

-0.0000 0.0000 0 0.0000 0 0.0000 0.0001

0.0000 0.0000 0.0000 0 0 -0.0000 0.0001

0.0001 0.0008 0 0 0 0.0010 0.0090

Columns 8 through 9

0.0000 0.0013

-0.0001 0.0175

0.0001 0.0125

-0.0010 3.7500

Press any key to continue ...

pivot row-> 1 pivot column-> 8

Tableau 6

A =

1.0e+005 *

Columns 1 through 7

-0.0000 -0.0000 0 0 0.0000 0.0000 -0.0000

-0.0000 -0.0000 0 0.0000 0.0000 0.0000 -0.0001

0.0000 0.0000 0.0000 0 -0.0000 -0.0000 0.0002

0.0001 0.0005 0 0 0.0004 0.0013 0.0060

Columns 8 through 9

0.0000 0.0005

0 0.0200

0 0.0100

0 3.8000

Press any key to continue ...

End of Phase 1

*********************************

Problem has a finite optimal solution

Values of the legitimate variables:

x(1)= 0.000000

x(2)= 0.000000

x(3)= 1000.000000

x(4)= 2000.000000

x(5)= 0.000000

Objective value at the optimal point:

z= 380000.000000

Gomoryho srihové riešenie

» type='max'

» c=[20 120 100 140 40]

» A=[0 0.4 0.3 0.6 0.6;0.05 0.2 0.1 0.1 0;0.1 0.2 0.2 0.1 0.2]

» b=[1500;300;450]

» cpa(type, c, A, b)

________________________________________________

Tableaux of the Simplex Algorithm

________________________________________________

Initial tableau

A =

1.0e+003 *

Columns 1 through 7

0 0.0004 0.0003 0.0006 0.0006 0.0010 0

0.0001 0.0002 0.0001 0.0001 0 0 0.0010

0.0001 0.0002 0.0002 0.0001 0.0002 0 0

-0.0200 -0.1200 -0.1000 -0.1400 -0.0400 0 0

Columns 8 through 9

0 1.5000

0 0.3000

0.0010 0.4500

0 0

Press any key to continue ...

Final tableau

A =

1.0e+005 *

Columns 1 through 7

-0.0000 -0.0000 0 0 0.0000 0.0000 -0.0000

-0.0000 -0.0000 0 0.0000 0.0000 0.0000 -0.0001

0.0000 0.0000 0.0000 0 -0.0000 -0.0000 0.0002

0.0001 0.0005 0 0 0.0004 0.0013 0.0060

Columns 8 through 9

0.0000 0.0005

0 0.0200

0 0.0100

0 3.8000

Press any key to continue ...

____________________________________________

Tableaux of the Dual Simplex Method

________________________________________________

pivot row-> 4 pivot column-> 2

Tableau 1

A =

1.0e+005 *

Columns 1 through 7

-0.0000 -0.0000 0 0 0.0000 0.0000 -0.0000

-0.0000 -0.0000 0 0.0000 0.0000 0.0000 -0.0001

0.0000 0.0000 0.0000 0 -0.0000 -0.0000 0.0002

0 -0.0000 0 0 0 -0.0000 0

0.0001 0.0005 0 0 0.0004 0.0013 0.0060

Columns 8 through 10

0.0000 0 0.0005

0 0 0.0200

0 0 0.0100

0 0.0000 -0.0000

0 0 3.8000

Press any key to continue ...

pivot row-> 5 pivot column-> 9

Tableau 2

A =

1.0e+005 *

Columns 1 through 7

-0.0000 0 0 0 0.0000 0.0000 -0.0000

-0.0000 0 0 0.0000 0.0000 0.0000 -0.0001

0.0000 0 0.0000 0 -0.0000 -0.0001 0.0002

0 0.0000 0 0 0 0.0000 0

0 0 0 0 0 0 0

0.0001 0 0 0 0.0004 0.0008 0.0060

Columns 8 through 11

0.0000 -0.0000 0 0.0005

0 -0.0000 0 0.0200

0 0.0000 0 0.0100

0 -0.0000 0 0.0000

0 -0.0000 0.0000 -0.0000

0 0.0008 0 3.7992

Press any key to continue ...

pivot row-> 6 pivot column->

Tableau 3

A =

1.0e+005 *

Columns 1 through 7

-0.0000 0 0 0 0.0000 0.0000 -0.0000

-0.0000 0 0 0.0000 0.0000 0.0000 -0.0001

0.0000 0 0.0000 0 -0.0000 -0.0001 0.0002

0 0.0000 0 0 0 0.0000 0

0 0 0 0 0 0 0

0 0 0 0 0 0 0

0.0001 0 0 0 0.0004 0.0008 0.0060

Columns 8 through 12

0.0000 0 -0.0000 0 0.0005

0 0 -0.0000 0 0.0200

0 0 0.0001 0 0.0099

0 0 -0.0000 0 0.0000

0 0.0000 -0.0000 0 0.0000

0 0 0 0.0000 -0.0000

0 0 0.0016 0 3.7984

Press any key to continue ...

Algorithm fails to find an optimal solution.

Celočíselné programovanie

Vyriešte úlohu:

Hľadáme vektor x = [x₁, x₂] ³ 0, s celočíselnými zložkami, vyhovujúci podmienkam

–3x₁+ 4x₂ £ 6

4x₁+ 3x₂ £ 12

a maximalizačný: z = x₁+ 2x₂

type = 'max';

c = [1 2];

A = [-3 4;4 3];

b = [6;12];

subs = dsimplex(type, c, A, b)

Initial tableau

A =

3 -4 1 0 -6

-4 -3 0 1 -12

-1 -2 0 0 0

Press any key to continue ...

pivot row-> 1 pivot column-> 2

Tableau 1

A =

-0.7500 1.0000 -0.2500 0 1.5000

-6.2500 0 -0.7500 1.0000 -7.5000

-2.5000 0 -0.5000 0 3.0000

Press any key to continue ...

pivot row-> 2 pivot column-> 3

Tableau 2

A =

1.3333 1.0000 0 -0.3333 4.0000

8.3333 0 1.0000 -1.3333 10.0000

1.6667 0 0 -0.6667 8.0000

Press any key to continue ...

Problem has a finite optimal solution

Values of the legitimate variables:

x(1)= 0.000000

x(2)= 4.000000

Objective value at the optimal point:

z= 8.000000

Indices of basic variables in the final tableau:

subs =

2

3

4.1 Oblasť použiteľnosti testovanej optimalizačnej metódy

Pri testovaní tejto optimalizačnej metódy sme prišli k záveru, že je vhodná najmä na riešenie klasických úloh lineárneho programovania, ktoré sú zadané účelovou funkcie a obmedzujúcimi podmienkami. Taktiež je týmto spôsobom možné riešiť aj niektroré úlohy celočíselného programovania, ktoré sú zadané ako linaárne problémy. Hodnoty premenných v takýchto úlohách musia však spĺňať podmienku prísnej celočíselnosti. Napriek tomu sa vyskytujú aj úlohy, pre ktoré pomocou linérneho programovania nemožno nájsť riešenie. V takom prípade je vhodné zvoliť inú optimalizačnú, ktorá bude schopná širšie riešiť daný problém.

Záver

Lineárne programovanie predstavuje pomerne malý úsek z širokej oblasti rôznych optimalizačných metód a úloh matematického programovania. Je to však oblasť, v ktorej možno jednoducho a rýchlo riešiť mnohé problémy ekonomického, technického a matematického charakteru. V lineárnom programovaní ide o optimalizačné úlohy, keď účelová funkcia a jej ohraničenia sú lineárne.

Cieľom tejto práce bolo priblížiť problematiku lineárneho programovania v prostredí MATLAB a otestovať túto metódu na konkrétnych príkladoch, na základe ktorých by bolo potom možné určiť oblasť uplatnenia zvolenej optimalizačnej metódy.

Pri voľbe optimalizačnej metódy bolo zistené, že úlohy lineárneho programovania je možné riešiť pomocou rôznych súborov programov. Z nich bolo vybrané na riešenie týchto problémov prostredie MATLAB. Jeho vhodnosť možno odôvodniť hlavne tým, že tento program získal široké uplatnenie preto, vďaka jeho dostupnosti a ovládateľnosti, keďže práca s ním je okrem iného súčasťou výučby.

V MATLAB-e sa pracuje s vektormi a maticam a to je výhodné aj pri riešení typických problémov lineárneho programovania. V práci sú uvedené jednotlivé funkcie, ktorými je v tomto programe možné riešiť úlohy lineárneho programovania. Rozdelené sú do jednotlivých kapitol, pričom v každej je popísaná metóda, ktorou je úloha lineárneho programovania v MATLAB-e riešená. Kompletné programy jednotlivých funkcií možno nájsť v prílohe k tejto práci. Pri každej metóde sú uvedené aj jednoduché príklady zápisu a riešenia jednotlivých úloh. Sú tam úlohy, ktoré zahŕňajú výpočet základných prípustných riešení, extrémnych bodov a extrémnych smerov pri daných obmedzujúcich podmienkach, geometrické riešenie problémov LP, ďalej úlohy pre dvojfázovú metódou, duálny simplexový algoritmus, prírastok obmedzení a Gomoryho strihový algoritmus. Postup výpočtu a tiež jednotlivé výsledky sa zobrazujú v prehľadných tabuľkách. Pri testovaní úloh lineárneho programovania sa našli aj problémy, ktoré nemali konečné riešenie alebo nespĺňali podmienky daných obmedzení. Ak takýto problém zadáme v MATLAB-e, program na túto skutočnosť upozorní pri výpočte, keď zistí, že úloha nevyhovuje podmienkam lineárneho programovania. Prípadne, ak daný problém sa rieši geometrickým spôsobom, zobrazí upozornenie, že hodnoty, s ktorými počíta , nie sú z prípustnej oblasti.

Na základe všeobecných poznatkov o linárnom programovaní a tiež testovania úloh lineárneho programovania môžeme povedať, že táto optimalizačná metóda, je vhodná najmä na riešenie klasických úloh LP, ale takisto ňou možno riešiť aj niektoré úlohy celočíselného programovania, ktoré musia spĺňať podmienku striktnej celočíselnosti premenných. Napriek tomu sme našli aj prípady, ktoré hoci mali splnenú uvedenú podmienku, neboli touto optimalizačnou metódou riešiteľné. V takom prípade je potrebné zvoliť niektorú inú metódu, ktorá by vyhovovala danej úlohe.

Použitá literatúra

[1] Neuman E.: Linear Programming with MATLAB, Tutorial 6, Math 472/CS 472, Department Of Mathematics, SIU, Carbondale, 2000

[2] www.math.siu.edu/matlab/tutorials.html

[3] Holström K., Björkman M. and Dotzauer E.: Applied Optimization and Modeling Group (TOM)², Department of Mathematics and Physics, Mälardalen University, Sweden, 1998

[4] Rychetník L., Zelinka J., Pelzauerová V.: Sbírka příkladů z lineárního programování, SNTL– Nakladatelství technické literatury, Praha, 1968

PRÍLOHY

Programy lineárneho programovania v prostredí MATLAB

Prílohy 1a, 1b, 1c, 1d a 1e sú pomocné funkcie MATLAB-u, uložené m-súboroch pomenovaných rovnako ako je aj názov danej funkcie.

Príloha č. 1a

function e = vr(m,i)

% Koordinačný vektor e v m-dimenzionálnom Euklidovskom priestore. I-tá

% zložka vektora

e = zeros(m,1);

e(i) = 1;

Príloha č. 1b

function d = delcols(d)

% Vymaže kópie stĺpcov matice d.

d = union(d',d','riadky')';

n = size(d,2);

j = [];

for k =1:n

c = d(:,k);

for l=k+1:n

if norm(c - d(:,l),'inf') <= 100*eps

j = [j l];

end

end

end

if ~isempty(j)

j = sort(j);

d(:,j) = [];

end

Príloha č. 1c

function [row, mi] = MRT(a, b)

% Test minimálneho pomeru (The Minimum Ratio Test (MRT)) uskutočnený na

% vektoroch a a b.

% Výstupné parametre:

% row - index určujúceho riadku

% mi - hodnota najmenšieho pomeru.

m = length(a);

c = 1:m;

a = a(:);

b = b(:);

l = c(b > 0);

[mi, row] = min(a(l)./b(l));

row = l(row);

Príloha č. 1d

function col = MRTD(a, b)

% Test maximálneho pomeru uskutočnený na vektoroch a a b.

% Táto funkcia je volaná z funkcie dsimplex.

% Výstupné parametre:

% col - index určujúceho stĺpca.

m = length(a);

c = 1:m;

a = a(:);

b = b(:);

l = c(b < 0);

[mi, col] = max(a(l)./b(l));

col = l(col);

Príloha č. 1e

function [m, j] = Br(d)

% Zaradenie Blandovho pravidla týkajúceho sa zoskupenia d.

% Výstupné parametre:

% m - prvé záporné číslo v zoskupení d

% j - index vstupného m.

% Táto funkcia je volaná z nasledujúcich funkcií:

% simplex2p, dsimplex, addconstr, simplex and cpa.

ind = find(d < 0);

if ~isempty(ind)

j = ind(1);

m = d(j);

else

m = [];

j = [];

end

Príloha č. 2 – funkcia počíta všetky základné prípustné riešenia, do systému obmedzení v štandardnej forme.

function vert = feassol(A, b)

% Základné prípustné riešenie konvertovať do systému obmedzení

% Ax = b, x >= 0.

% Sú uložené v stĺpcoch konvertovanej matice.

[m, n] = size(A);

warning off

b = b(:);

vert = [];

if (n >= m)

t = nchoosek(1:n,m);

nv = nchoosek(n,m);

for i=1:nv

y = zeros(n,1);

x = A(:,t(i,:))\b;

if all(x >= 0 & (x ~= inf & x ~= -inf))

y(t(i,:)) = x;

vert = [vert y];

end

end

else

error('Číslo z rovnice musí byť väčšie ako číslo premennej.')

end

if ~isempty(vert)

vert = delcols(vert);

else

vert = [];

end

Príloha č. 3a – funkcia na výpočet extrémnych bodov.

function vert = extrpts(A, rel, b)

% Extrémne body konvertované polyédrickou množinou

% X = {x: Ax <= b alebo Ax >= b, x >= 0}.

% Znaky nerovnosti sú uložené v príkaze rel, e.g.,

% rel = '<<>' reprezentujú <= , <= , a >= , jednotlivo.

[m, n] = size(A);

nlv = n;

for i=1:m

if(rel(i) == '>')

A = [A -vr(m,i)];

else

A = [A vr(m,i)];

end

if b(i) < 0

A(i,:) = - A(i,:);

b(i) = -b(i);

end

end

warning off

[m, n]= size(A);

b = b(:);

vert = [];

if (n >= m)

t = nchoosek(1:n,m);

nv = nchoosek(n,m);

for i=1:nv

y = zeros(n,1);

x = A(:,t(i,:))\b;

if all(x >= 0 & (x ~= inf & x ~= -inf))

y(t(i,:)) = x;

vert = [vert y];

end

end

else

error('Číslo z rovnice musí byť väčšie ako číslo premennej')

end

vert = delcols(vert);

vert = vert(1:nlv,:);

Príloha č. 3b – funkcia počítajúca extrémne smery.

function d = extrdir(A, rel, b)

% Extrémne smery d polyédrickej množiny

% X = {x: Ax <= b, or Ax >= b, x >= 0}.

% Matica A musí mať plný počet riadkov.

[m, n] = size(A);

n1 = n;

for i=1:m

if(rel(i) == '>')

A = [A -vr(m,i)];

else

A = [A vr(m,i)];

end

end

[m, n] = size(A);

A = [A;ones(1,n)];

b = [zeros(m,1);1];

d = feassol(A,b);

if ~isempty(d)

d1 = d(1:n1,:);

d = delcols(d1);

s = sum(d);

for i=1:n1

d(:,i) = d(:,i)/s(i);

end

else

d = [];

end

Príloha č. 4 – funkcia pre grafické riešenie lineárnych úloh.

function drawfr(c, A, rel, b)

% Grafy prípustnej oblasti a čiara úrovne problému LP s dvomi

% premennými

%

% min (max)z = c*x

% Za predpokladu,že: Ax <= b (or Ax >= b),

% x >= 0

clc

[m, n] = size(A);

if n ~= 2

str = 'Číslo premennej musí byť rovné 2';

msgbox(str,'Chybné Okno','error')

return

end

t = extrpts(A,rel,b);

if isempty(t)

disp(sprintf('\n Prázdna prípustná oblasť'))

return

end

t = t(1:2,:);

t = delcols(t);

d = extrdir(A,rel,b);

if ~isempty(d)

msgbox('Neohraničená prípustná oblasť','Výstražné Okno','warn')

disp(sprintf('\n Extrémny smer(y) zo súboru obmedzení'))

d

disp(sprintf('\n Extrémny bod zo súboru obmedzení'))

t

return

end

t1 = t(1,:);

t2 = t(2,:);

z = convhull(t1,t2);

hold on

patch(t1(z),t2(z),'r')

h = .25;

mit1 = min(t1)-h;

mat1 = max(t1)+h;

mit2 = min(t2)-h;

mat2 = max(t2)+h;

if c(1) ~= 0 & c(2) ~= 0

sl = -c(1)/c(2);

if sl > 0

z = c(:)'*[mit1;mit2];

a1 = [mit1 mat1];

b1 = [mit2 (z-c(1)*mat1)/c(2)];

else

z = c(:)'*[mat1;mit2];

a1 = [mit1 mat1];

b1 = [(z-c(1)*mit1)/c(2) mit2];

end

elseif c(1) == 0 & c(2) ~= 0

z = 0;

a1 = [mit1 mat1];

b1 = [0,0];

else

z = 0;

a1 = [0 0];

b1 = [mit2 mat2];

end

h = plot(a1,b1);

set(h,'druh čiary','--')

set(h,'hrúbka čiary',2)

str = 'Prípustná oblasť a úroveň čiary s objektívnou hodnotou = ';

title([str,num2str(z)])

axis([mit1 mat1 mit2 mat2])

h = get(gca,'Názov');

set(h,'Veľkosť písma',11)

xlabel('x_1')

h = get(gca,'x menovka');

set(h,'Veľkosť písma',11)

ylabel('x_2')

h = get(gca,'y menovka');

set(h,'Veľkosť písma',11)

grid

hold off

Príloha č. 5a– funkcia na riešenie dvojfázovej metódy.

function simplex2p(type, c, A, rel, b)

% Dvojfázová metóda ne riešenie problému LP

% min(alebo max) z = c*x

% Za predpokladu,že: Ax rel b

% x >= 0

% Typ vstupných parametrov nesie informácie o type riešeného problému LP.

% Typ pre minimalizačný problém = 'min'

% Typ pre maximalizačný problém = 'max'.

% Vstupný parameter rel je príkaz nesúci znaky vzťahov.

% Napríklad, ak rel = '<=>', potom systém obmedzení pozostáva z

% jednej nerovnosti <=, jednej rovnosti, a jednej nerovnosti>=.

if (type == 'min')

mm = 0;

else

mm = 1;

c = -c;

end

b = b(:);

c = c(:)';

[m, n] = size(A);

n1 = n;

les = 0;

neq = 0;

red = 0;

if length(c) < n

c = [c zeros(1,n-length(c))];

end

for i=1:m

if(rel(i) == '<')

A = [A vr(m,i)];

les = les + 1;

elseif(rel(i) == '>')

A = [A -vr(m,i)];

else

neq = neq + 1;

end

end

ncol = length(A);

if les == m

c = [c zeros(1,ncol-length(c))];

A = [A;c];

A = [A [b;0]];

[subs, A, z, p1] = loop(A, n1+1:ncol, mm, 1, 1);

disp(' Koniec fázy 1')

disp(' *********************************')

else

A = [A eye(m) b];

if m > 1

w = -sum(A(1:m,1:ncol));

else

w = -A(1,1:ncol);

end

c = [c zeros(1,length(A)-length(c))];

A = [A;c];

A = [A;[w zeros(1,m) -sum(b)]];

subs = ncol+1:ncol+m;

av = subs;

[subs, A, z, p1] = loop(A, subs, mm, 2, 1);

if p1 == 'y'

disp(' Koniec fázy 1')

disp(' *********************************')

end

nc = ncol + m + 1;

x = zeros(nc-1,1);

x(subs) = A(1:m,nc);

xa = x(av);

com = intersect(subs,av);

if (any(xa) ~= 0)

disp(sprintf('\n\n Prázdna prípustná oblasť\n'))

return

else

if ~isempty(com)

red = 1;

end

end

A = A(1:m+1,1:nc);

A =[A(1:m+1,1:ncol) A(1:m+1,nc)];

[subs, A, z, p1] = loop(A, subs, mm, 1, 2);

if p1 == 'y'

disp(' Koniec fázy 2')

disp(' *********************************')

end

end

if (z == inf | z == -inf)

return

end

[m, n] = size(A);

x = zeros(n,1);

x(subs) = A(1:m-1,n);

x = x(1:n1);

if mm == 0

z = -A(m,n);

else

z = A(m,n);

end

disp(sprintf('\n\n Problém má konečné optimálne riešenie\n'))

disp(sprintf('\n Hodnota premennej:\n'))

for i=1:n1

disp(sprintf(' x(%d)= %f ',i,x(i)))

end

disp(sprintf('\n Hodnota v optimálnom bode:\n'))

disp(sprintf(' z= %f',z))

t = find(A(m,1:n-1) == 0);

if length(t) > m-1

str = 'Problém má nekonečne veľa riešení';

msgbox(str,'Výstražné Okno','warn')

end

if red == 1

disp(sprintf('\n Systém obmedzení je prebytočný\n\n'))

end

Príloha č. 5b – funkcia je zahrnutá vo funkcii simplex2p, zabraňuje cyklovaniu.

function [subs, A, z, p1]= loop(A, subs, mm, k, ph)

% Hlavná slučka simplexového primárneho algoritmu.

% Použité Blandovo pravidlo zabraňujúce zacyklovaniu.

tbn = 0;

str1 = 'Chceš monitorovať priebeh výpočtu fázy 1?';

str2 = 'Chceš monitorovať priebeh výpočtu fázy 2?';

if ph == 1

str = str1;

else

str = str2;

end

question_ans = questdlg(str,'Urob výber v Okne','Yes','No','No');

if strcmp(question_ans,'Yes')

p1 = 'y';

end

if p1 == 'y' & ph == 1

disp(sprintf('\n\n Počiatočná tabuľka'))

A

disp(sprintf(' Pokračuj stlačením ľubovolnej klávesy ...\n\n'))

pause

end

if p1 == 'y' & ph == 2

tbn = 1;

disp(sprintf('\n\n Tabuľka %g',tbn))

A

disp(sprintf(' Pokračuj stlačením ľubovolnej klávesy ...\n\n'))

pause

end

[m, n] = size(A);

[mi, col] = Br(A(m,1:n-1));

while ~isempty(mi) & mi < 0 & abs(mi) > eps

t = A(1:m-k,col);

if all(t <= 0)

if mm == 0

z = -inf;

else

z = inf;

end

disp(sprintf('\n Neohraničené optimálne riešenie s z= %s\n',z))

return

end

[row, small] = MRT(A(1:m-k,n),A(1:m-k,col));

if ~isempty(row)

if abs(small) <= 100*eps & k == 1

[s,col] = Br(A(m,1:n-1));

end

if p1 == 'y'

disp(sprintf(' kľúčový riadok-> %g kľúčový stĺpec-> %g',... row,col))

end

A(row,:)= A(row,:)/A(row,col);

subs(row) = col;

for i = 1:m

if i ~= row

A(i,:)= A(i,:)-A(i,col)*A(row,:);

end

end

[mi, col] = Br(A(m,1:n-1));

end

tbn = tbn + 1;

if p1 == 'y'

disp(sprintf('\n\n Tabuľka %g',tbn))

A

disp(sprintf(' Pokračuj stlačením ľubovolnej klávesy...\n\n'))

pause

end

end

z = A(m,n);

Príloha č. 6 – funkcia vypočíta optimálne riešenie optimalizačného problému.

function varargout = dsimplex(type, c, A, b)

% Duálny simplexový algoritmus riešiaci problémy LP

% min (max) z = c*x

% Za predpokladu,že: Ax >= b

% x >= 0

%

if type == 'min'

mm = 0;

else

mm = 1;

c = -c;

end

str = 'Chceš monitorovať priebeh výpočtu?';

A = -A;

b = -b(:);

c = c(:)';

[m, n] = size(A);

A = [A eye(m) b];

A = [A;[c zeros(1,m+1)]];

question_ans = questdlg(str,'Urob v okne nasledujúci výber','Yes','No','No');

if strcmp(question_ans,'Yes')

p1 = 'y';

else

p1 = 'n';

end

if p1 == 'y'

disp(sprintf('\n\n Počiatočná tabuľka'))

A

disp(sprintf(' Pokračuj stlačením ľubovolnej klávesy...\n\n'))

pause

end

subs = n+1:n+m;

[bmin, row] = Br(b);

tbn = 0;

while ~isempty(bmin) & bmin < 0 & abs(bmin) > eps

if A(row,1:m+n) >= 0

disp(sprintf('\n\n Prázdna prípustná oblasť\n'))

varargout(1)={subs(:)};

varargout(2)={A};

varargout(3) = {zeros(n,1)};

varargout(4) = {0};

return

end

col = MRTD(A(m+1,1:m+n),A(row,1:m+n));

if p1 == 'y'

disp(sprintf(' kľúčový riadok-> %g kľúčový stĺpec-> %g',...

row,col))

end

subs(row) = col;

A(row,:)= A(row,:)/A(row,col);

for i = 1:m+1

if i ~= row

A(i,:)= A(i,:)-A(i,col)*A(row,:);

end

end

tbn = tbn + 1;

if p1 == 'y'

disp(sprintf('\n\n Tabuľka %g',tbn))

A

disp(sprintf(' Pokračuj stlačením ľubovolnej klávesy...\n\n'))

pause

end

[bmin, row] = Br(A(1:m,m+n+1));

end

x = zeros(m+n,1);

x(subs) = A(1:m,m+n+1);

x = x(1:n);

if mm == 0

z = -A(m+1,m+n+1);

else

z = A(m+1,m+n+1);

end

disp(sprintf('\n\n Problém má konečné optimálne riešenie\n\n'))

disp(sprintf('\n Hodnota premennej:\n'))

for i=1:n

disp(sprintf(' x(%d)= %f ',i,x(i)))

end

disp(sprintf('\n Hodnota v optimálnom bode:\n'))

disp(sprintf(' z= %f',z))

disp(sprintf('\n Indexy základných premenných v konečnej tabuľke:'))

varargout(1)={subs(:)};

varargout(2)={A};

varargout(3) = {x};

varargout(4) = {z};

Príloha č. 7 – funkcia zlepšujúca citlivosť analýzy riešenia problému pridaním obmedzení.

function addconstr(type, A, subs, a, rel, d)

% Pridanie obmedzenia do konečnej tabuľky A.

% Vstupné parametre nesú indexy základných premenných spojených s tab. A.

% Parametre lhs, rel, and rhs nesú informácie o pridaní:

% a - koeficienty legitímnych premenných

% rel – príkaz nesúci znaky nerovnosti;

% napríklad, rel = '<' reprezentuje <=.

% d - konštantná hodnota pridaných obmedzení.

% Typ parametra je string, ktorý opisuje typ optimalizačného problému.

% Pre typ minimalizačného problému= 'min' a pre typ maximalizačného

% problému = 'max'.

clc

str = 'Chceš monitorovať priebeh výpočtu?';

question_ans=questdlg(str,'Urob v okne nasledujúci výber','Yes','No','No');

if strcmp(question_ans,'Yes')

p1 = 'y';

else

p1 = 'n';

end

[m, n] = size(A);

a = a(:)';

lc = length(a);

if lc < n-1

a = [a zeros(1,n-lc-1)];

end

if type == 'min'

ty = -1;

else

ty = 1;

end

x = zeros(n-1,1);

x(subs) = A(1:m-1,n);

dp = a*x;

if (dp <= d & rel == '<') | (dp >= d & rel == '>')

disp(sprintf('\n\n Problém má konečné optimálne riešenie\n'))

disp(sprintf('\n Hodnota premennej:\n'))

for i=1:n-1

disp(sprintf(' x(%d)= %f ',i,x(i)))

end

disp(sprintf('\n Hodnota v optimálnom bode:\n'))

disp(sprintf(' z= %f',ty*A(m,n)))

return

end

B = [A(:,1:n-1) zeros(m,1) A(:,n)];

if rel == '<'

a = [a 1 d];

else

a = [a -1 d];

end

for i=1:m-1

a = a - a(subs(i))*B(i,:);

end

if a(end) > 0

a = -a;

end

A = [B(1:m-1,:);a;B(m,:)];

if p1 == 'y'

disp(sprintf('\n\n Počiatočná tabuľka'))

A

disp(sprintf(' Pokračuj stlačením ľubovolnej klávesy...\n\n'))

pause

end

[bmin, row] = Br(A(1:m,end));

tbn = 0;

while ~isempty(bmin) & bmin < 0 & abs(bmin) > eps

if A(row,1:n) >= 0

disp(sprintf('\n\n Prázdna prípustná oblasť\n'))

return

end

col = MRTD(A(m+1,1:n),A(row,1:n));

if p1 == 'y'

disp(sprintf(' kľúčový riadok-> %g kľúčový stĺpec-> %g',... row,col))

end

subs(row) = col;

A(row,:)= A(row,:)/A(row,col);

for i = 1:m+1

if i ~= row

A(i,:)= A(i,:)-A(i,col)*A(row,:);

end

end

tbn = tbn + 1;

if p1 == 'y'

disp(sprintf('\n\n Tabuľka %g',tbn))

A

disp(sprintf(' Pokračuj stlačením ľubovolnej klávesy ...\n\n'))

pause

end

[bmin, row] = Br(A(1:m,end));

end

x = zeros(n+1,1);

x(subs) = A(1:m,end);

x = x(1:n);

disp(sprintf('\n\n Problém má konečné optimálne riešenie\n\n'))

disp(sprintf('\n Hodnota premennej:\n'))

for i=1:n

disp(sprintf(' x(%d)= %f ',i,x(i)))

end

disp(sprintf('\n Hodnota v optimálnom bode:\n'))

disp(sprintf(' z= %f',ty*A(m+1,n+1)))

Príloha č. 8a – funkcie na riešenie úloh celočíselného programovania.

function cpa(type, c, A, b)

% Gomoryho strihový stupňový algoritmus pre riešenie

% problému celočíselného programovania

% min(max) z = c*x

% Za predpokladu,že: Ax <= b

% x >= 0 a celočíselné

str = 'Chceš monitorovať priebeh výpočtu?';

question_ans=questdlg(str,'Urob v Okne nasledujúci výber','Yes','No','No');

if strcmp(question_ans,'Yes')

p1 = 'y';

else

p1 = 'n';

end

if type == 'min'

tp = -1;

else

tp = 1;

end

[m,n] = size(A);

nlv = n;

b = b(:);

c = c(:)';

if p1 == 'y'

[A,subs] = simplex(type,c,A,b,p1);

else

[A,subs] = simplex(type,c,A,b);

end

[m,n] = size(A);

d = A(1:m-1,end);

pc = fractp(d);

tbn = 0;

if p1 == 'y'

disp(sprintf(' ________________________________________________'))

disp(sprintf('\n Tabuľka duálnej simplexovej metódy'))

disp(sprintf(' ________________________________________________'))

end

while norm(pc,'inf') > eps

[el,i] = max(pc);

nr = A(i,1:n-1);

nr = [-fractp(nr) 1 -el];

B = [A(1:m-1,1:n-1) zeros(m-1,1) A(1:m-1,end)];

B = [B;nr;[A(m,1:n-1) 0 A(end,end)]];

A = B;

[m,n] = size(A);

[bmin, row] = Br(A(1:m-1,end));

while ~isempty(bmin) & bmin < 0 & abs(bmin) > eps

col = MRTD(A(m,1:n-1),A(row,1:n-1));

if p1 == 'y'

disp(sprintf('\n kľúčový riadok-> %g kľúčový stĺpec-> %g',... row,col))

tbn = tbn + 1;

disp(sprintf('\n Tabuľka %g',tbn))

A

disp(sprintf(' Pokračuj stlačením ľubovolnej klávesy ...\n'))

pause

end

if isempty(col)

disp(sprintf('\n Algoritmus nemôže nájsť optimálne riešenie.'))

return

end

subs(row) = col;

A(row,:)= A(row,:)./A(row,col);

for i = 1:m

if i ~= row

A(i,:)= A(i,:)-A(i,col)*A(row,:);

end

end

[bmin, row] = Br(A(1:m-1,end));

end

d = A(1:m-1,end);

pc = fractp(d);

end

if p1 == 'y'

disp(sprintf('\n Konečná tabuľka'))

A

disp(sprintf(' Pokračuj stlačením ľubovolnej klávesy ...\n'))

pause

end

x = zeros(n-1,1);

x(subs) = A(1:m-1,end);

x = x(1:nlv);

disp(sprintf('\n Problém má konečné optimálne riešenie\n\n'))

disp(sprintf('\n Hodnota premennej:\n'))

for i=1:nlv

disp(sprintf(' x(%d)= %g ',i,x(i)))

end

disp(sprintf('\n Hodnota v optimálnom bode:\n'))

disp(sprintf(' z= %f',tp*A(m,n)))

Príloha č. 8b

function y = fractp(x)

% Zlomková časť y z x, keď x je matica.

y = zeros(1,length(x));

ind = find(abs(x - round(x)) >= 100*eps);

y(ind) = x(ind) - floor(x(ind));

Príloha č. 8c

function[A, subs, x, z] = simplex(type, c, A, b, varargin);

% Simplexový algoritmus pre ptroblémy LP

% min(max) z = c*x

% Za predpokladu,že: Ax <= b

% x >= 0

% Vektor b musí byť kladný.

% Pre typ minimalizačného problému string = 'min',

% inak typ = 'max'.

% Piaty vstupný parameter je voliteľný. Ak je to množina ´y´, tak

% počitočná a konečná tabuľka je zobrazená na obrazovke.

% Výstupné parametre:

% A - konečná tabuľka simplexovej metódy

% subs - indexy základných premenných v konečnej tabuľke

% x - optimálne riešenie

% z - hodnota objektívnej funkcie v x.

if any(b < 0)

error(' Pravé strany množimy obmedzení musia byť kladné.')

end

if type == 'min'

tp = -1;

else

tp = 1;

c = -c;

end

[m, n] = size(A);

A = [A eye(m)];

b = b(:);

c = c(:)';

A = [A b];

d = [c zeros(1,m+1)];

A = [A;d];

if nargin == 5

disp(sprintf(' ________________________________________________'))

disp(sprintf('\n Tabuľka Simplexového algoritmu'))

disp(sprintf(' ________________________________________________'))

disp(sprintf('\n Počiatočná tabuľka\n'))

A

disp(sprintf(' Pokračuj stlačením ľubovolnej klávesy ...\n\n'))

pause

end

[mi, col] = Br(A(m+1,1:m+n));

subs = n+1:m+n;

while ~isempty(mi) & mi < 0 & abs(mi) > eps

t = A(1:m,col);

if all(t <= 0)

disp(sprintf('\n Problém má neohraničenú objektívnu funkciu'));

x = zeros(n,1);

if tp == -1

z = -inf;

else

z = inf;

end

return;

end

row = MRT(A(1:m,m+n+1),A(1:m,col));

if ~isempty(row)

A(row,:)= A(row,:)/A(row,col);

subs(row) = col;

for i = 1:m+1

if i ~= row

A(i,:)= A(i,:)-A(i,col)*A(row,:);

end

end

end

[mi, col] = Br(A(m+1,1:m+n));

end

z = tp*A(m+1,m+n+1);

x = zeros(1,m+n);

x(subs) = A(1:m,m+n+1);

x = x(1:n)';

if nargin == 5

disp(sprintf('\n\n Konečná tabuľka'))

A

disp(sprintf(' Pokračuj stlačením ľubovolnej klávesy ...\n'))

pause

end