12. Ďalšie možnosti MATLABu

12.1. Lokálne funkcie

Do jedného súboru je možné umiestniť viac funkcií, t.j. viac funkcií začínajúcich kľúčovým slovom function. Tieto funkcie sú potom lokálne vzhľadom k súboru - sú "viditeľné" iba z ostatných funkcií v súbore a je možné ich používať iba v nich. Prvá funkcia v súbore je tzv. primárna a iba táto funkcia je prístupná "z vonku". Táto vlastnosť je užitočná napr. v situácii, keď sa nejaká funkcia niekoľkokrát používa, ale nijaká iná funkcia ju nebude potrebovať.

Príklad 12.1: Funkcia, ktorá vypisuje faktoriál zadaného čísla (faktorial.m)

function faktorial(n)
% FAKTORIAL - vypocet a vypis faktorialu celeho cisla (n!)
% faktorial(n)   
% n ... cislo

if n<0
  error('faktorial neexistuje')
end
y = 1; 
for i=1:n
    y = y*i;    
end
vypis(n,y)

% Lokalna funkcia

function vypis(a,b)
% VYPIS - vypis faktorialu celeho cisla
% a ... cislo   
% b ... faktorial(a)
y = sprintf('%d! = %d',a,b);
disp(y);

Výsledok príkladu 12.1:

>> faktorial(5)
5! = 120

top

12.2. Viacrozmerné matice a objektová orientácia

Okrem základných typov - char (string), uint8, double a sparse MATLAB od verzie 5 zavádza nové dátové typy cell (cell array) a struct (struct array). Zavedenie týchto dátových štruktúr súvisí s prechodom na objekty.

12.2.1. Pole buniek

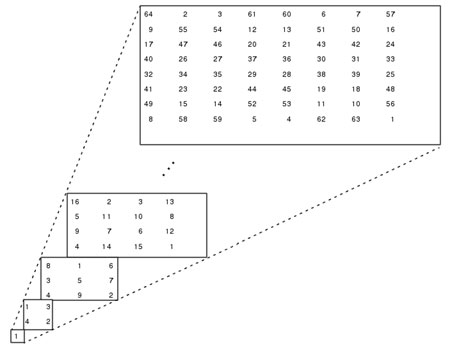
Cell array (pole buniek) je dátová štruktúra odpovedajúca viacrozmernej matici. Vytvoriť premennú tohto typu je možné funkciou cell alebo pomocou zložených zátvoriek {}. V poli buniek možno kombinovať rôzne dátové typy.

Syntax príkazu:

cell(m, n, p, ...)

Vytvára m x n x p x ... pole buniek prázdnych matíc. Argumenty m, n, p, ... musia byť skaláry.

Príklad 12.5: Pole buniek prázdnych matíc (2x3x2)

>> C = cell(2,3,2)
C(:,:,1) = 
     []     []     []
     []     []     []
C(:,:,2) = 
     []     []     []
     []     []     []

Príklad 12.6: Naplnenie poľa buniek

>> for n = 1:12
   C{n} = n;
   end

>> C
C(:,:,1) = 
    [1]    [3]    [5]
    [2]    [4]    [6]
C(:,:,2) = 
    [7]    [ 9]    [11]
    [8]    [10]    [12]

Výsledok príkladu 12.6: Vypísanie niektorých častí poľa buniek

>> C(1,2,1)
ans = 
    [3]

>> C(:,2,1)
ans = 
    [3]
    [4]
>> C(:,2,2)
ans = 
    [ 9]
    [10]

Príklad 12.7: Iný spôsob vytvorenia poľa buniek

>> CC = {pi 'Ahoj' magic(3); 5 C 7}
CC = 
    [3.1416]    'Ahoj'          [3x3 double]
    [     5]    {2x3x2 cell}    [         7]

Príklad 12.8: Vypísanie obsahu poľa buniek: celldisp

>> celldisp(CC)
CC{1,1} =
    3.1416
CC{2,1} =
     5
CC{1,2} =
Ahoj
CC{2,2}{1,1,1} =
     []
CC{2,2}{1,2,1} =
     []
CC{2,2}{1,1,2} =
     []
CC{2,2}{1,2,2} =
     []
CC{1,3} =
     8     1     6
     3     5     7
     4     9     2
CC{2,3} =
     7

Príklad 12.9: Grafické zobrazenie štruktúry poľa buniek: cellplot

>> cellplot(CC)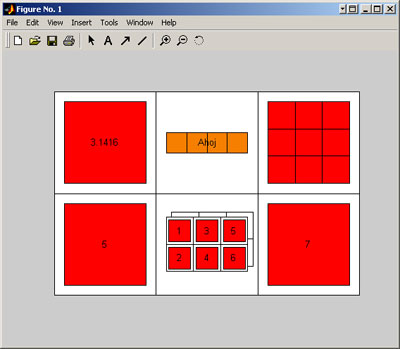

Príklad 12.10: Sekvencia "magických" matíc rôznych stupňov

>> cell(8,1);
>> for n = 1:8
   M{n} = magic(n);
   end
>> M
    [         1]
    [2x2 double]
    [3x3 double]
    [4x4 double]
    [5x5 double]
    [6x6 double]
    [7x7 double]
    [8x8 double]

Výsledok príkladu 12.10:

12.2.2. Pole štruktúr

Structure array (pole štruktúr) odpovedá priamo významu štruktúry používanej v programovacích jazykoch. Jednotlivé prvky poľa sú pomenované. Štruktúru možno vytvoriť funkciou struct alebo naplnením jednotlivých položiek.

Syntax príkazu:

s = struct('položka1', {}, 'položka2', {}, ...)
s = struct('položka', hodnota1, 'položka2', hodnota2, ...)

s = struct('položka1', {}, 'položka2', {}, ...) vytvára prázdne pole štruktúr položka1, položka2, ....
s = struct('položka1', hodnota1, 'položka2', hodnota2, ...) vytvára pole štruktúr so špecifikovanými položkami a hodnotami. Hodnoty hodnota1, hodnota2, atď. musia byť polia buniek rovnakej veľkosti alebo bunky so skalármi.

Príklad 12.11: Pole štruktúr

>> student = struct('meno',{'Ján','Jozef','Milan'},'priezvisko', ...
{'Novak','Sovak','Liska'},'rocnik',{1,2,5})

student = 
1x3 struct array with fields:
    meno
    priezvisko
    rocnik

Výsledok príkladu 12.11:

>> student(1)
ans = 
          meno: 'Ján'
    priezvisko: 'Novak'
        rocnik: 1

>> student(2)
ans = 
          meno: 'Jozef'
    priezvisko: 'Sovak'
        rocnik: 2

>> student(3)
ans = 
          meno: 'Milan'
    priezvisko: 'Liska'
        rocnik: 5

Príklad 12.12: Doplnenie hodnôt

>> student(4).meno = 'Michal';
student = 

1x4 struct array with fields:
    meno
    priezvisko
    rocnik

>> student(4)
ans = 
          meno: 'Michal'
    priezvisko: []
        rocnik: []

Výsledok príkladu 12.12:

% prístup k menu 1. študenta
>> student(1).meno
ans =
Ján
% prístup k priezvisku 1. študenta
>> student(1).priezvisko
ans =
Novak

% prístup k ročníku 2. študenta
>> student(2).rocnik
ans =
     2
	
% prístup k menu 3. študenta
>> student(3).meno
ans =
Milan

Príklad 12.13: Iný spôsob vytvorenia poľa štruktúr

>> skuska(1).predmet = 'Optimalizácia' 
skuska = 
    predmet: 'Optimalizácia'

>> skuska(1).datum = [20 12 2005]
skuska = 
    predmet: 'Optimalizácia'
      datum: [20 12 2005]

% prístup k roku 1. skúšky  
>> skuska(1).datum(3)
ans =
        2005

top

12.3. Riešenie nelineárnych rovníc

Na riešenie nelineárnych rovníc metódou najmenších štvorcov môžeme použiť funkciu fsolve. Fsolve rieši rovnice v tvare F(X) = 0, kde F a X môžu byť vektory alebo matice.

Syntax funkcie: X = fsolve(funkcia,XO)
Funkcia rieši rovnice vo funkcii funkcia s počiatočnými hodnotami X0.

Úplný zápis funkcie: [X,FVAL,EXITFLAG] = fsolve(FUN,X0,OPTIONS,P1,P2,...), kde

pomocou funkcie optimset nastavujeme parametre štruktúry OPTIONS. Parametrami funkcie optimset sú Display, TolX, TolFun, DerivativeCheck, Diagnostics, Jacobian, JacobMult, JacobPattern, LineSearchType, LevenbergMarquardt, MaxFunEvals, MaxIter, DiffMinChange and DiffMaxChange, LargeScale, MaxPCGIter, PrecondBandWidth, TolPCG, TypicalX
P1,P2,... sú parametre "predávané" funkcii funkcia
FVAL "vracia" hodnotu funkcie funkcia
EXITFLAG informuje o konvergencii, resp. divergencii riešenia (1 - konverguje)

Príklad

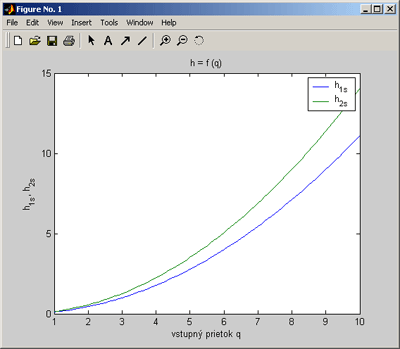
Úlohou je zistiť ustálené výšky hladín h_1s a h_2s dvoch zásobníkov (zapojených za sebou bez interakcie) pre vstupný prietok q_s = 6 do prvého z nich.

Príklad 12.14: Funkcia zasob.m

function y = zasob(h,q)
k1 = 3; f1 = 3; 
k2 = 2.4; f2 = 2.7;
y(1) = q/f1 - k1/f1*sqrt(h(1));
y(2) = k1/f1*sqrt(h(1)) - k2/f2*sqrt(h(2));

Výsledok príkladu 12.14: Riešenie pre q_s = 6

>> [h,FVAL,EXITFLAG] = fsolve('zasob',[2;2],optimset('Display','iter'),6)

                                         Norm of      First-order   Trust-region
 Iteration  Func-count     f(x)          step         optimality    radius
     0          3        0.367837                         0.152               1
     1          6        0.198685              1         0.0975               1
     2          9      0.00687788        2.39651         0.0167             2.5
     3         12     6.0457e-006        0.49403       0.000586            5.99
     4         15    2.70656e-012      0.0129899      4.11e-007            5.99
Optimization terminated: first-order optimality is less than options.TolFun.

h =
    4.0000
    5.0625
FVAL =
  1.0e-005 *
    0.0003    0.1645
EXITFLAG =
     1

Výsledok príkladu 12.14: Graf ustálených výšok pre prietoky q_s = 1 až 10

top

12.4. Úlohy

Majme binárny súbor data.mat, v ktorom je uložená premenná získaná zo simulácie (viď. obrázok).
Analyzujte uvedenú premennú (štruktúru) a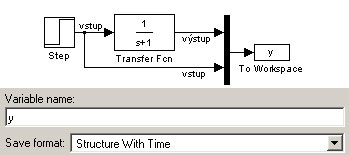
- vykreslite do jedného grafu (do troch podokien) priebeh vstupnej(1), výstupnej(2), vstupnej a výstupnej(3) veličiny (bloku Function Fcn) v závislosti od času (viď. ukážka);
  
  1
  
  vstup = f(čas) 2
  
  výstup = f(čas)
  
  3
  
  vstup, výstup = f(čas)
- popíšte časové osi: time [s];
- popíšte názvy grafov: 1) vstup; 2) výstup; 3) vstup a výstup;
- zobrazte legendu v 3. podokne: --- vstup x₁, -.- výstup x₂
Zistite ustálenú hodnotu výšky hladiny v zásobníku (h_s) opísaného diferenciálnou rovnicou

dh/dt = q/f₁ - k₁/f₁*h^0.5, kde k₁ = 3, f₁ = 3 a ustálený prietok q_s = 5.

Poznámka: index s označuje ustálené hodnoty.
Riešte sústavu nelineárnych rovníc

0 = 0.8 - x + (1-x)*e^(y)
0 = 5 - 2*y + (2-x)*e^1/y

top

1 vstup = f(čas)	2 výstup = f(čas)
3 vstup, výstup = f(čas)