6. Polynómy

6.1. Polynomické funkcie

Funkcia	Opis
conv	násobenie polynómov
deconv	delenie polynómov
poly	konštrukcia polynómov zo špecifikovaných koreňov
polyder	derivácia polynómu
polyfit	aproximácia dát polynómom
polyval	hodnota polynómu
polyvalm	hodnota polynómu s maticovým argumentom
residue	rozklad na parciálne zlomky
roots	nájdenie koreňov polynómu

Všeobecne polynóm p vieme zapísať nasledovne: p = [p₁ p₂ ... p_n p_n+1], čo vyjadruje p = p₁sⁿ+p₂s^n-1+ ... p_ns+ p_n+1].

Jednotlivé funkcie uvedené v tabuľke si ukážeme na príkladoch.

6.1.1. Násobenie a delenie polynómov

Príklad 6.1: Súčin polynómov

>> b = [1 4 5 2]; a = [2 5 3];
>> conv(a,b)
ans =
     2    13    33    41    25     6

Príklad 6.2: Delenie polynómov

>> [q,r] = deconv(b,a)
q =
    0.5000    0.7500
r =
    0         0   -0.2500   -0.2500
% Spätná kontrola 
>> conv(q,a)+r
ans =
     1     4     5     2

6.1.2. Hodnota polynómu

Nech p = [p₁ p₂ ... p_n p_n+1], potom funkciu y = polyval(p,x) je získaná z výrazu y = p₁xⁿ+p₂x^n-1+ ... p_nx+p_n+1

Príklad 6.3: Skalár

>> p = [2 3 4 1];
>> polyval(p,1)
ans =
    10

Príklad 6.4: Vektor

>> polyval(p,[0 2 3])
ans =
     1    37    94

6.1.3. Korene polynómu

Príklad 6.5: Korene polynómu x³+2x²-9x-18

>> roots([1 2 -9 -18])
ans =
    3.0000
   -3.0000
   -2.0000

Príklad 6.6: Korene polynómu z³-2z²+3z+5

>> roots([1 -2 3 5])
ans =
   1.4473 + 1.8694i
   1.4473 - 1.8694i
  -0.8946

6.1.4. Charakteristický polynóm matice

Príklad 6.7:

>> A = [1.2 3 -0.9;5 1.75 6;9 0 1];
>> poly(A)
ans =
    1.0000   -3.9500   -1.8500 -163.2750

6.1.5. Vytvorenie polynómu na základe jeho koreňov

Príklad 6.8:

>> a = [1.2 3 -0.9 0 1];
>> poly(a)
ans =
    1.0000   -4.3000    3.1200    3.4200   -3.2400   0
% Spätná kontrola 
>> roots(ans)
ans =
         0
    3.0000
   -0.9000
    1.2000
    1.0000

6.1.6. Derivácia polynómu

Príklad 6.9: Derivácia polynómu

>> a = [2 1 3];
>> polyder(a)
ans =
     4     1

>> b = [3 1 5 4];
>> polyder(b)
ans =
     9     2     5

Príklad 6.10: Derivácia súčinu polynómov a*b

>> polyder(a,b)
ans =
    30    20    60    32    19

Príklad 6.11: Derivácia podielu polynómov b/a ako podiel q/d

>> [q,d] = polyder(b,a)
q =
     6     6    18   -10    11
d =
     4     4    13     6     9

6.1.7. Rozklad polynómov na parciálne zlomky

B/A = R(1)/(s-P(1)) + R(2)/(s-P(2)) + ... R(n)/(s-P(n)) + K

Príklad 6.12:

>> a = [1 5.5 -1.5 -27]; b = [2 5 1];
>> [R,P,K] = residue(b,a)
R =
    1.9487
   -0.5333
    0.5846
P =
   -4.5000
   -3.0000
    2.0000
K =
     []

6.1.8. Aproximácia dát polynómom n-tého stupňa

V MATLABe je možné zadané (namerené) údaje aproximovať polynómom n-tého stupňa pomocou funkcie polyfit, ktorá používa metódu najmenších štvorcov (MNŠ):

Syntax príkazu:

p = polyfit(x,y,n)

kde

x je vektor hodnôt nezávislej premennej,
y je vektor hodnôt závislej premennej,
n je stupeň polynómu, ktorým chceme aproximovať body [xi,yi]
p je vektor koeficientov výsledného polynómu P(x), pričom P(x) = p(1)xⁿ + p(2)x^n-1 + ... + p(n)x + p(n+1)

Poznámka:

voľba stupňa polynómu väčšinou závisí na fyzikálnej podstate prolému
pokiaľ pre údaje dĺžky N použijeme polynóm stupňa N-1, vykonávame aproximáciu interpolaciou (t.j. polynóm bude prochádzať všetkými bodmi [xi,yi])
pre polynóm stupňa N (a vyššieho) úloha samozrejme nemá jednoznačné riešenie a funkcia polyfit hlási "Warning"
pokiaľ potrebujeme aproximovať inou funkciou než polynomom, je možné M-súbor funkcie polyfit upraviť (a uložiť pod iným názvom) alebo použiť MNŠ, ktorá vedie na riešenie sústavy lineárnych rovníc. Uvedené postupy je možné samozrejme použiť iba pre modely, ktoré sú lineárne v parametroch!

Pretože nás okrem koeficientov aproximovaného polynómu väčšinou zaujímajú aj hodnoty polynómu P(x) vo všetkých prvkoch vektora x (napr. kvôli grafickému znázorneniu), existuje tiež funkcia polyval:

Syntax príkazu:

y_aprox = polyval(p,x)

kde

p je vektor koeficientov aproximovaného polynómu,
x je vektor hodnôt nezávislej premennej
y_aprox je vektor hodnôt aproximovaného polynómu.

Príklad 6.13: Aproximácia namerených hodnôt polynómom 2. stupňa

% namerene udaje, nezavisl. premenne
>> u = [1 1.5 2.1 2.5 3 3.1 3.2 3.5];
% namerene udaje, zavisl. premenne
>> v = [7.8 8.15 8.3 8.25 8.1 8.3 8.35 8.2]; 
>> p1 = polyfit(u,v,2)       % koeficienty polynomu 2. stupna pre 'u' a 'v'
p1 =
   -0.1629    0.8665    7.1462

>> v_aprox = polyval(p1,u);  % hodnoty polynómu pre 'u'
>> Sv = sum((v_aprox-v).^2)  % suma stvorcov odchyliek
Sv =
    0.0556

Príklad 6.14: Aproxiácia priamkou

>> p2 = polyfit(u,v,1)       % koeficienty polynomu 1. stupna pre 'u' a 'v'
p2 =
    0.1313    7.8547
>> p_aprox = polyval(p2,u);  % hodnoty polynómu pre 'u'
>> Sp = sum((p_aprox-v).^2)  % suma stvorcov odchyliek
Sp =
    0.1198

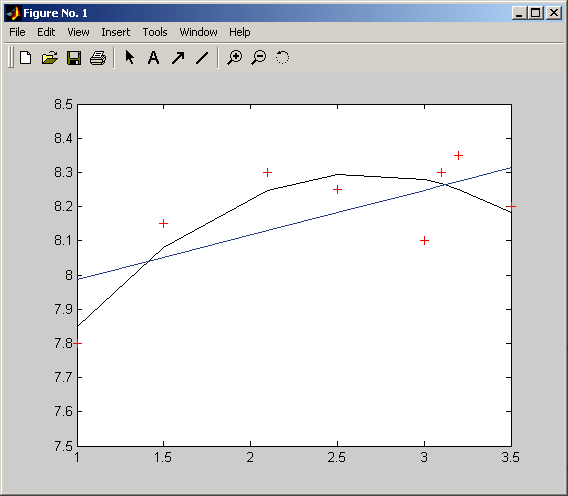
Príklad 6.15: Vykreslenie aproximácie polynómom 1. a 2. stupňa

>> plot(u,v,'r+')        % graf, povodne udaje ako cervene kriziky 
>> hold on               % prikreslenie dalsich udajov
>> plot(u,v_aprox,'k')   % graf polynomu 2. stupna (cierne body spojene ciarou)
>> plot(u,p_aprox,'b')   % graf polynomu 1. stupna (modre body spojene ciarou)

Výsledok príkladu 6.15:

top

6.2. Úlohy

Vyvorte polynómy:
- a = 2x³-3x+1
- b = 3x²+7x+2
- c = x-3
Vyskúšajte operácie násobenia a delenia polynómov:
- vynásobte polynómy a*b, b*c, a*c
- vydeľte polynómy a/b
Vypočítajte nasledovné derivácie polynómov:
- deriváciu polynómu a
- deriváciu súčinu polynómov b, c
- deriváciu podielu polynómov a, c
Zistite korene polynómov a, b
Vypočítajte hodnoty polynómov a, b pre vstupné hodnoty [1 2 3]
Aproximujte údaje x, y polynómami 2. až 5. stupňa ak:
x = [1:10];
y = [-4 -7 4 41 116 241 428 689 1036 1481];
- vypočítajte sumy štvorcov odchyliek
- ktorá aproximácia je najlepšia? (na vyhodnotenie použite príkaz pre vetvenie)

top