16. S-funkcia
S-funkcia je dynamický blok v Simulinku, ktorého "opis" je definovaný vo funkcii-súbore vytvoreného v MATLABe, v jazykoch C, C++, Ada, alebo Fortran. S-funkcie vytvorené v jazykoch C, C++, Ada a Fortran sú kompilované na MEX-súbory (pozri "Building MEX-Files" v dokumentácii). My sa budeme venovať S-funkciam vytvoreným v MATLABe.
S-funkcia umožňuje užívateľovi vytvárať vlastné bloky do modelu v Simulinku. V m-súbore S-funkcie môžu byť definované vlastné diferenciálne rovnice (ordinary differential equations (ODEs)), rovnice diskrétneho systému a/alebo ľubovoľný typ algoritmu.
16.1. Použitie S-funkcie v modeloch
Blok S-function sa nachádza v knižnici Simulink->User-Defined Functions (Simulink v. 5.0, v iných verziách: Simulink->Functions & Tables). Po presunutí/skopírovaní bloku do modelu sa definuje názov S-funkcie v položke S-function name (obr. 1).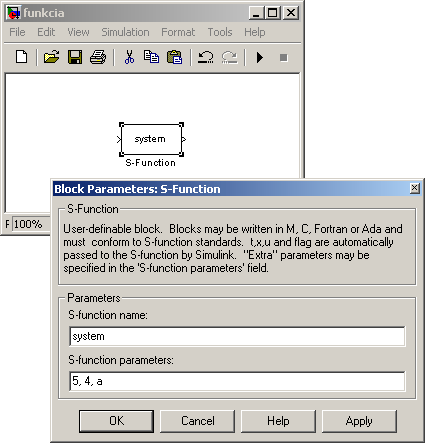
Obr. 1. Blok S-function
Do položky S-function parameters sa zadávajú parametre "prenášané" do S-funkcie. Jednotlivé parametre sa oddeľujú čiarkou. Parametrami môžu byť konštanty (vektory, matice), názvy premenných definovaných v pracovnom priestore MATLABu, alebo výrazy v MATLABe (obr. 1). Parametre t,x,u (čas, stavy, vstupy) sú Simulinkom automaticky "prenášané" do S-funkcie.
16.2. Ako S-funkcia pracuje
S-funkcia reprezentuje dynamický blok
u -> [ x ] -> y vstup systém (stavy) výstup
kde výstupy sú funkciou periódy vzorkovania, vstupov a stavov. Matematické vzťahy medzi vstupmi, výstupmi a stavmi môžu byť vyjadrené nasledujúcimi rovnicami:
y = f_y(t,x,u) (výstup)
x_s = f_s(t,x,u) (derivácia - spojitý systém)
x_d(t+1) = f_d(t,x,u) (diferencia - diskrétny systém)
x = {x_s, x_d}
"Spracovanie/simulácia" S-funkcie prebieha v niekoľkých etapách:
- flag = 0 - inicializácia (funkcia mdlInitializeSizes)
- flag = 4 - výpočet periódy vzorkovania (funkcia mdlGetTimeOfNextVarHit)
- flag = 3 - výpočet výstupu y (funkcia mdlOutputs)
- flag = 2 - výpočet diskrétnych stavov x_d (funkcia mdlUpdate)
- flag = 1 - výpočet spojitých stavov x_s (funkcia mdlDerivatives)
- flag = 9 - koniec (funkcia mdlTerminate)
S-funkcia v tvare m-súboru je definovaná ako obyčajná funkcia v MATLABe:
function [sys,x0,str,ts] = meno(t,x,u,flag)
V prípade, že S-funkcia vyžaduje ďalšie vstupné parametre, jej tvar je nasledujúci:
function [sys,x0,str,ts] = meno(t,x,u,flag,p1,p2,...)
kde meno je názov S-funkcie, t je aktuálny čas, x je vektor stavov daného bloku (S-funkcie), u sú vstupy do bloku, flag udáva vykonávanú úlohu a p1, p2, ... sú parametre bloku. Počas simulácie modelu, Simulink opakovane vyvoláva S-funkciu meno a na základe flagov sa vykonávajú jednotlivé etapy S-funkcie.
Poznámka: v adresári toolbox\simulink\blocks\ sa nachádzajú príklady spojitej (csfunc.m) a diskrétnej (dsfunc.m) s-funkcie
Štruktúra S-funkcie bude vysvetlená na príklade šablóny sfuntmpl.m (help sfuntmpl, type sfuntmpl):
function [sys,x0,str,ts] = sfuntmpl(t,x,u,flag)
switch flag,
%%%%%%%%%%%%%%%%%%
% Initialization %
%%%%%%%%%%%%%%%%%%
case 0,
[sys,x0,str,ts]=mdlInitializeSizes;
%%%%%%%%%%%%%%%
% Derivatives %
%%%%%%%%%%%%%%%
case 1,
sys=mdlDerivatives(t,x,u);
%%%%%%%%%%
% Update %
%%%%%%%%%%
case 2,
sys=mdlUpdate(t,x,u);
%%%%%%%%%%%
% Outputs %
%%%%%%%%%%%
case 3,
sys=mdlOutputs(t,x,u);
%%%%%%%%%%%%%%%%%%%%%%%
% GetTimeOfNextVarHit %
%%%%%%%%%%%%%%%%%%%%%%%
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
%%%%%%%%%%%%%
% Terminate %
%%%%%%%%%%%%%
case 9,
sys=mdlTerminate(t,x,u);
%%%%%%%%%%%%%%%%%%%%
% Unexpected flags %
%%%%%%%%%%%%%%%%%%%%
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
% end sfuntmpl
%
%==========================================================================
% mdlInitializeSizes
% Return the sizes, initial conditions, and sample times for the S-function.
%==========================================================================
%
function [sys,x0,str,ts]=mdlInitializeSizes
%
% call simsizes for a sizes structure, fill it in and convert it to a
% sizes array.
%
% Note that in this example, the values are hard coded. This is not a
% recommended practice as the characteristics of the block are typically
% defined by the S-function parameters.
%
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 0;
sizes.NumInputs = 0;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1; % at least one sample time is needed
sys = simsizes(sizes);
%
% initialize the initial conditions
%
x0 = [];
%
% str is always an empty matrix
%
str = [];
%
% initialize the array of sample times
%
ts = [0 0];
% end mdlInitializeSizes
%
%==========================================================================
% mdlDerivatives
% Return the derivatives for the continuous states.
%==========================================================================
%
function sys=mdlDerivatives(t,x,u)
sys = [];
% end mdlDerivatives
%
%==========================================================================
% mdlUpdate
% Handle discrete state updates, sample time hits, and major time step
% requirements.
%==========================================================================
%
function sys=mdlUpdate(t,x,u)
sys = [];
% end mdlUpdate
%
%==========================================================================
% mdlOutputs
% Return the block outputs.
%==========================================================================
%
function sys=mdlOutputs(t,x,u)
sys = [];
% end mdlOutputs
%
%==========================================================================
% mdlGetTimeOfNextVarHit
% Return the time of the next hit for this block. Note that the result is
% absolute time. Note that this function is only used when you specify a
% variable discrete-time sample time [-2 0] in the sample time array in
% mdlInitializeSizes.
%==========================================================================
%
function sys=mdlGetTimeOfNextVarHit(t,x,u)
sampleTime = 1; % Example, set the next hit to be one second later.
sys = t + sampleTime;
% end mdlGetTimeOfNextVarHit
%
%==========================================================================
% mdlTerminate
% Perform any end of simulation tasks.
%==========================================================================
%
function sys=mdlTerminate(t,x,u)
sys = [];
% end mdlTerminate
Definovanie periódy vzorkovania: (ts)
ts = [0 0] (spojitý systém) ts = [-1 0] (zdedená ts, offset) ts = [1 0] (diskrétny systém, ts = 1) ts = [0 0; 1 0] (hybridny systém (spojitý + diskrétny systém))
Pri zdedenej perióde vzorkovania sa perióda vzorkovania "dedí" z predchádzajúceho, alebo nasledujúceho bloku, alebo je použitá najrýchlejšia perióda vzorkovania.
Definovanie počiatočných hodnôt stavov: (x0)
x0 = [] (systém nemá stavy) x0 = zeros(1,n) (systém má n stavov ( = 0)) % length(x0) = length(sizes.NumContStates) (spojitý systém) % length(x0) = length(sizes.NumDiscStates) (diskrétny systém)
Definovanie veľkosti vstupov/výstupov: (sizes.NumOutputs, sizes.NumInputs)
sizes.NumOutputs = 0; (nie je výstup) sizes.NumInputs = 0; (nie je vstup) sizes.NumOutputs = 2; (2 výstupy) sizes.NumInputs = 3; (3 vstupy) sizes.NumOutputs = -1; (výstupy s dynamickou veľkosťou) sizes.NumInputs = -1; (vstupy s dynamickou veľkosťou) % veľkosť vektora vstupu (sizes.NumInputs = length(u))
Definovanie priamej väzby (Direct feedthrough): (sizes.DirFeedthrough)
sizes.DirFeedthrough = 0; sizes.DirFeedthrough = 1;
sizes.DirFeedthrough = 1 znamená, že výstup (flag == 3) alebo premenlivá perióda vzorkovania (flag == 4) je priamo funkciou vstupu (u), inak sizes.DirFeedthrough = 0.
Definovanie sizes.NumSampleTimes:
Ak sizes.NumSampleTimes > 0, potom S-funkcia má "block-based sample times".
16.2.1. Príklad: hydraulický systém
Postup tvorby S-funkcie bude vysvetlený na príklade modelu hydraulického systému popísaného diferenciálnymi rovnicami (rovnice sú zapísané vo formáte TeX):
\dot{h}_1 = 1/F1 u - k1/F1 sqrt ( h(1) - h(2) )
\dot{h}_2 = k1/F2 sqrt ( h(1) - h(2) ) - k2/F2 sqrt ( h(2) )
function [sys,x0,str,ts] = hyd2(t,x,u,flag)
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes;
case 1,
sys=mdlDerivatives(t,x,u);
case 3,
sys=mdlOutputs(t,x,u);
case {2, 4, 9},
sys = [];
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
%==========================================================================
% mdlInitializeSizes
%==========================================================================
function [sys,x0,str,ts]=mdlInitializeSizes
h1s=1; h2s=1; % definovanie ustálených výšok hladín
sizes = simsizes;
sizes.NumContStates = 2; % dva stavy (výška h1 a h2)
sizes.NumDiscStates = 0;
sizes.NumOutputs = 1; % jeden výstup (výška h2)
sizes.NumInputs = 1; % jeden vstup (prietok)
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = [h1s; h2s];
str = [];
ts = [0 0];
%==========================================================================
% mdlDerivatives
%==========================================================================
function sys=mdlDerivatives(t,x,u)
f1=1; f2=1; k1=1; k2=1; % definovanie parametrov zásobníkov
% Matematický model hydraulického systému v tvare diferenciálnych rovníc
sys(1) = 1/f1*u-k1/f1*sqrt(x(1)-x(2));
sys(2) = k1/f2*sqrt(x(1)-x(2))-k2/f2*sqrt(x(2));
sys = [sys(1); sys(2)];
%==========================================================================
% mdlOutputs
%==========================================================================
function sys=mdlOutputs(t,x,u)
sys = x(2); % Výstupom je druhý stav (výška h2)
V S-funkcii hyd2.m sú parametre f1,f2,k1,k2,h1s,h2s definované priamo.
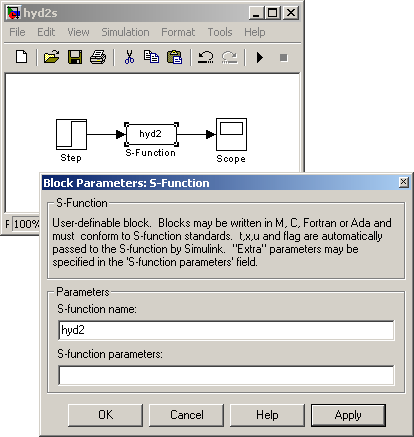
Obr. 2. S-funkcia hyd2.m s priamo definovanými parametrami
V nasledujúcej funkcii sa parametre f1,f2,k1,k2,h1s,h2s funkcii predávajú.
function [sys,x0,str,ts] = hyd2m(t,x,u,flag,ff,kk,hs)
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes(hs(1),hs(2));
case 1,
sys=mdlDerivatives(t,x,u,ff(1),ff(2),kk(1),kk(2));
case 3,
sys=mdlOutputs(t,x,u);
case {2, 4, 9},
sys = [];
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
%==========================================================================
% mdlInitializeSizes
%==========================================================================
function [sys,x0,str,ts]=mdlInitializeSizes(h1s,h2s)
sizes = simsizes;
sizes.NumContStates = 2;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 1;
sizes.NumInputs = 1;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = [h1s; h2s];
str = [];
ts = [0 0];
%==========================================================================
% mdlDerivatives
%==========================================================================
function sys=mdlDerivatives(t,x,u,f1,f2,k1,k2)
sys(1) = 1/f1*u-k1/f1*sqrt(x(1)-x(2));
sys(2) = k1/f2*sqrt(x(1)-x(2))-k2/f2*sqrt(x(2));
sys = [sys(1); sys(2)];
%==========================================================================
% mdlOutputs
%==========================================================================
function sys=mdlOutputs(t,x,u)
sys = x(2);
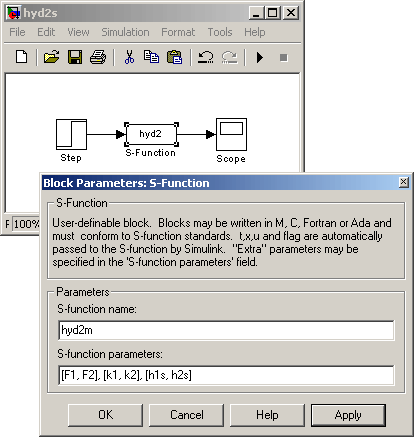
Obr. 3. Nemaskovaná S-funkcia hyd2m
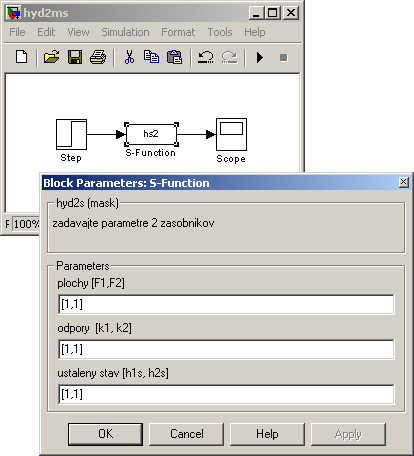
Obr. 4. Maskovaná S-funkcia hyd2m
16.2.2. Príklad:
Demoverzia S-funkcie, ktorej výstup je dvojnásobkom jej vstupu (y = 2 * u).
function [sys,x0,str,ts] = timestwo(t,x,u,flag)
switch flag,
case 0
[sys,x0,str,ts]=mdlInitializeSizes;
case 3
sys=mdlOutputs(t,x,u);
case { 1, 2, 4, 9 }
sys=[];
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
%==========================================================================
% mdlInitializeSizes
%==========================================================================
function [sys,x0,str,ts] = mdlInitializeSizes()
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 0;
sizes.NumOutputs = -1; % dynamically sized
sizes.NumInputs = -1; % dynamically sized
sizes.DirFeedthrough = 1; % has direct feedthrough
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
str = [];
x0 = [];
ts = [-1 0]; % inherited sample time
%==========================================================================
% mdlOutputs
%==========================================================================
function sys = mdlOutputs(t,x,u)
sys = u * 2;
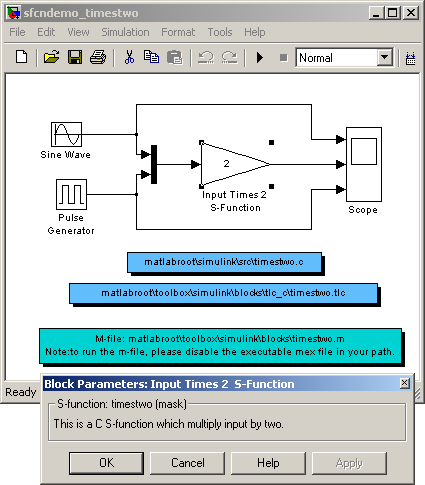
Obr. 5. Model s S-funkciou timestwo.m
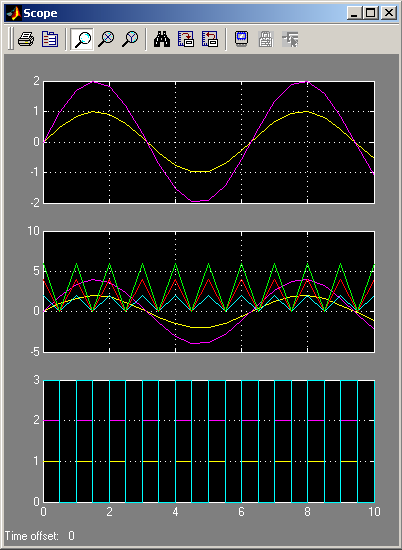
Obr. 6. Priebeh simulácie s S-funkciou timestwo.m
16.3. Úlohy
- Vytvorte m-súbor S-funkcie modelu dvoch zásobníkov kvapaliny. Parametre zásobníkov kvapaliny
sú [k1, k2, f1, f2, q0s] =
[9.0, 8.28, 9.0, 7.83, 9.0]. Parametre sa zadávajú pomocou
masky S-funkcie.
Matematický model zásobníkov kvapaliny s interakciou
dh1/dt = 1/F1 * q0 - k1/F1 * (h1 - h2)0.5
dh2/dt = k1/F2 * (h1 - h2)0.5 - k2/F2 * (h2)0.5Matematický model zásobníkov kvapaliny bez interakcie
dh1/dt = 1/F1 * q0 - k1/F1 * (h1)0.5
dh2/dt = k1/F2 * (h1)0.5 - k2/F2 * (h2)0.5Poznámka: začiatočné hodnoty výšok hladín závisia od typu (s/bez interakcie).
- Výber zásobníkov s interakciou/bez interakcie urobte pomocou checkboxu
- V prípade, že niektorý z parametrov nie je definovaný (t.j. je definovaný prázdny vektor/matica []), použije sa jeho predvolená hodnota a vypíše sa hlásenie o uvedenej zmene
- Simulujte priebeh výšok hladín zásobníkov pri zmene prietoku q0 z ustálenej hodnoty q0s na hodnotu o 5% väčšiu