5. Matice a vektory
V názve matice, ktorý môže obsahovať až 31 znakov, sú povolené iba nasledujúce znaky:
- písmená anglickej abecedy (a-z, A-Z)
- číslice (0-9)
- podtrhovník (_)
Názov nesmie začínať číslicou.
5.1. Zápis matice
Maticu rozmeru mxn vytvárame pomocou hranatých zátvoriek, v ktorých uvádzame jednotlivé riadky oddelené bodkočiarkou, pričom prvky každého riadku (stĺpce) oddeľujeme medzerou alebo čiarkou (môžme ich použiť aj naraz). V každom riadku musí byť rovnaký počet prvkov (stĺpcov)!
5.1.1. Spôsoby zadávania matice
Rôzne spôsoby zadávania matice si ukážeme na príkladoch. Majme maticu
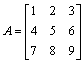
>> A = [1 2 3;4 5 6;7 8 9]
A =
1 2 3
4 5 6
7 8 9
>> A = [1,2,3;4,5,6;7,8,9]
A =
1 2 3
4 5 6
7 8 9
>> A = [1,2,3
4,5,6
7,8,9]
A =
1 2 3
4 5 6
7 8 9
>> A = [1 2 3;4,5,6
7 8 9]
A =
1 2 3
4 5 6
7 8 9
>> A(1,2) = 0
A =
1 0 3
4 5 6
7 8 9
>> B(1,2) = 3 % B(riadok, stĺpec) = hodnota
B =
0 3
>> B(3,3) = 4
B =
0 3 0
0 0 0
0 0 4
>> B(2,2:3) = [1 2]
B =
0 3 0
0 1 2
0 0 4
5.2. Manipulácia s maticami
5.2.1. Výber prvkov a nejakej časti matice
Rôzne spôsoby manipulácie matice si opäť ukážeme na príkladoch. Majme maticu
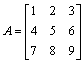
>> B = A(2,2)
B =
5
>> A(1,3)
ans =
3
>> B = A(2,:) % Výraz : znamená všetky stĺpce B = 4 5 6 >> A(:,3) % Výraz : znamená všetky riadky ans = 3 6 9
>> B = A(2:3,1:2) % Výraz n:m znamená B = % n-tý riadok (stĺpec) až m-tý riadok (stĺpec) 4 5 7 8 >> A(1,1:2) ans = 1 2
>> a = [1 2 3 4 5 6 7 8 9 0 1 2 3]
a =
1 2 3 4 5 6 7 8 9 0 1 2 3
>> a(1:end) % Výraz end posledný prvok (index)
ans =
1 2 3 4 5 6 7 8 9 0 1 2 3
>> a(4:end-2)
ans =
4 5 6 7 8 9 0 1
5.2.2. Funkcie pre manipuláciu s maticami
Medzi užitočné funkcie patria tiež tie, ktoré manipulujú s maticami/vektormi. Môžu nám uľahčiť prácu so zadávaním matíc/vektorov.
| Funkcia | Opis |
|---|---|
| diag | vytvorenie a vybratie diagonály matice |
| fliplr | výmena stĺpcov matice zľava-doprava |
| flipud | výmena riadkov matice zhora-nadol |
| rot90 | rotácia matice o 90 stupňov |
| size | rozmery matice |
| tril | vybratie dolnej triangulárnej matice |
| triu | vybratie hornej triangulárnej matice |
| : | index v matici |
Použitie funkcií pre manipuláciu s maticami, ktoré sú uvedené v tabuľke, si opäť ukážeme na príkladoch. Majme maticu a vektor
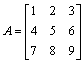
>> d = diag(A)
d =
1
5
9
>> d = diag(A,-1)
d =
4
8
>> d = diag(A,1)
d =
2
6
>> d = diag(A,2)
d =
3
>> D = diag(b)
D =
1 0 0 0 0
0 2 0 0 0
0 0 3 0 0
0 0 0 4 0
0 0 0 0 5
>> B = fliplr(A)
B =
3 2 1
6 5 4
9 8 7
>> B = flipud(A)
B =
7 8 9
4 5 6
1 2 3
>> size(A)
ans =
3 3
>> [riadky, stlpce] = size(A)
riadky =
3
stlpce =
3
>> B = rot90(A) % Rotácia matice o 90º
B =
3 6 9
2 5 8
1 4 7
>> B = tril(A)
B =
1 0 0
4 5 0
7 8 9
>> B = tril(A,-1)
B =
0 0 0
4 0 0
7 8 0
>> B = triu(A)
B =
1 2 3
0 5 6
0 0 9
>> B = triu(A,1)
B =
0 2 3
0 0 6
0 0 0
5.3. Maticové operácie
Všetky premenné sú v MATLABe chápané ako matice. S tým súvisí aj správanie sa operátorov.
| Názov | Syntax | Opis |
|---|---|---|
| sčítanie | a1+a2 |
|
| odčítanie | a1-a2 | |
| násobenie matíc | a1*a2 |
|
| umocnenie matice | a1^a2 |
|
| delenie matíc | a1/a2 |
|
| delenie matíc zľava | a1\a2 |
|
| transpozícia a konjugovanosť | a1' |
|
5.3.1. Príklady pre základné maticové operácie
>> C = [1 2;7 8];
>> D = [3 -5;-1 4];
>> C+D
ans =
4 -3
6 12
>> 3+D
ans =
6 -2
2 7
>> C-D
ans =
-2 7
8 4
>> D-2
1 -7
-3 2
>> b = [2;6];
>> C*D
ans =
1 3
13 -3
>> C*b % Rozmery: 2x2 x 2x1 » 2x1
ans =
14
62
>> D*2
ans =
6 -10
-2 8
>> A = [1 2;7 8];
>> B = [3 -5;-1 4];
>> x = B/A
x =
-9.8333 1.8333
6.0000 -1.0000
>> x = A\B
x =
-4.3333 8.0000
3.6667 -6.5000
>> C'
ans =
1 7
2 8
C^2
ans =
15 18
63 78
% Rovnaký výsledok dosiahneme aj výrazom
C*C
ans =
15 18
63 78
5.3.2. Operácie po prvkoch v maticových zápisoch
| Názov | Syntax | Opis |
|---|---|---|
| sčítanie | a1+a2 | |
| odčítanie | a1-a2 | |
| násobenie po prvkoch | a1.*a2 | |
| umocnenie po prvkoch | a1.^a2 | |
| delenie po prvkoch | a1./a2 | |
| delenie po prvkoch zľava | a1.\a2 |
>> C.*D
ans =
3 -10
-7 32
>> C./D
ans =
0.3333 -0.4000
-7.0000 2.0000
>> C.^2
ans =
1 4
49 64
>> C.*C
ans =
1 4
49 64
5.3.3. Riešenie sústavy lineárnych rovníc
Sústavu rovníc Ax = b riešime pomocou operátora \ alebo pomocou inverznej matice (funkcie inv). V každom prípade je potreba najskôr overiť rešiteľnosť sústavy, napríklad pomocou výpočtu determinantu (funkcie det):
function x = sustava(A,b) % SUSTAVA - riesenie sustavy linearnych rovnic % A ... matice sustavy % b ... vektor pravych stran % x ... riesenie sustavy if det(A) == 0 error('Sustava nema riesenie!') end x = A\b; % vypocet riesenia alebo x=inv(A)*b;
>> M=[3 2 -1; 1 0 1; 2 1 -1]; % zadanie sustavy v maticovem tvare >> v=[5;4;2]; >> riesenie = sustava(M,v) % spustenie funkcie riesenie = 1.5000 1.5000 2.5000 >> M*riesenie % overenie spravnosti riesenia ans = 5 4 2
5.3.4. Operácie v cykle
Ak je potrebné vektor naplniť prvkami, ktoré sú od seba rovnako "vzdialené", je možné to urobiť pomocou "dvojbodkového priradenia", x = [xzac:dx:xkon] kde xzac je začiatočná hodnota, dx je inkrement a xkon je konečná hodnota.
% Vytvorenie vektora s prvkami od 0 po 3 delením 0.5
x = [0:0.5:3]
x =
0 0.5 1 1.5 2 2.5 3
% Vytvorenie vektora s prvkami od 10 po 15 delením 1
y = 10:15
y =
10 11 12 13 14 15
5.4. Špeciálne matice
Medzi užitočné funkcie patria tiež tie, ktoré vytvárajú matice/vektory. Môžu nám uľahčiť prácu so zadávaním matíc/vektorov. Tieto funkcie majú väčšinou dva vstupné parametre: [matica] = nazov_funkcie(m,n), ale pokiaľ chceme získať štvorcovú maticu (typu mxm), stačí zadať iba jeden vstup. Prehľad týchto funkcií zobrazí príkaz help elmat.
| funkcia | Opis |
|---|---|
| eye | jednotková diagonálna matica |
| zeros | nulová matica |
| ones | matica zložená z jednotiek |
| rand | matica náhodných čísel z intervalu (0,1) |
| randn | matica náhodných čísel |
| linspace | vektor hodnôt s lineárnym delením |
| logspace | vektor hodnôt s logaritmickým delením |
| magic | magická štvorcová matica |
| meshgrid | X a Y súradnice pre 3-D zobrazenie |
>> C = eye(3) % alebo C = eye(3,3)
C =
1 0 0
0 1 0
0 0 1
>> C = zeros(2,3)
C =
0 0 0
0 0 0
>> C = ones(3,2)
C =
1 1
1 1
1 1
>> rand(2,3)
ans =
0.4447 0.7919 0.7382
0.6154 0.9218 0.1763
>> randn(2,3)
ans =
-0.5883 -0.1364 1.0668
2.1832 0.1139 0.0593
>> linspace(1,3) % 100 bodov v intervale <1,3> ans = Columns 1 through 7 1.0000 1.0202 1.0404 1.0606 1.0808 1.1010 1.1212 Columns 8 through 14 1.1414 1.1616 1.1818 1.2020 1.2222 1.2424 1.2626 ... Columns 99 through 100 2.9798 3.0000 >> linspace(1,3,10) % 10 bodov v intervale <1,3> ans = Columns 1 through 7 1.0000 1.2222 1.4444 1.6667 1.8889 2.1111 2.3333 Columns 8 through 10 2.5556 2.7778 3.0000
>> logspace(1,3)
ans =
1.0e+003 *
Columns 1 through 7
0.0100 0.0110 0.0121 0.0133 0.0146 0.0160 0.0176
Columns 8 through 14
0.0193 0.0212 0.0233 0.0256 0.0281 0.0309 0.0339
...
Columns 99 through 100
2.9798 3.0000
>> linspace(1,3,10) % 10 bodov v intervale <1,3>
ans =
1.0e+003 *
Columns 1 through 7
0.0100 0.0167 0.0278 0.0464 0.0774 0.1292 0.2154
Columns 8 through 10
0.3594 0.5995 1.0000
% Magicka matica: sucet kazdeho riadka a stlpca a diagonály je rovnaky >> magic(4) % magic(n) - musi platit n >= 3 ans = 16 2 3 13 5 11 10 8 9 7 6 12 4 14 15 1
>> [X,Y] = meshgrid(-2:.2:2, -2:.2:2);
>> size(X)
ans =
21 21
>> size(Y)
ans =
21 21
>> length(-2:.2:2)
ans =
21
Asys = [zeros(3,1), eye(3); -1,-3,-5,-8]
Asys =
0 1 0 0
0 0 1 0
0 0 0 1
-1 -3 -5 -8
5.5. Úlohy
- Vytvorte ľubovoľnú maticu A o rozmere 3x3, vyskúšajte si rôzne spôsoby zápisu
- S maticou A urobte nasledovné úkony:
- vyberte prvok prvého riadku a druhého stĺpca
- vyberte prvky druhého riadku a druhého až tretieho stĺpca
- vyberte prvky prvého riadku
- vyberte prvky tretieho stĺpca
- vyberte hlavnú diagonálu
- zistite rozmery matice
- rotujte maticu o 90 stupňov
- Vytvorte dve matice rovnakých rozmerov a skúste urobiť ich súčet a rozdiel
- Vytvorte si štvorcovú maticu, urobte jej transpozíciu a umocnite na druhú
- Vytvorte si dve štvorcové matice a vynásobte ich
- Operácie umocnenia a násobenia vyskúšajte aj po prvkoch
- Riešte sústavu rovníc
2x1 + 5x2 + 3x3 = 1
4x1 + 6x2 + 2x3 = 5
x1 - 5x2 + 3x3 = 3 - Vytvorte vektor s hodnotami od 10 do 30 s delením 3
- Vytvorte si nasledovné špecialne matice:
- jednotkovú diagonálnu maticu rozmerov 3x3
- nulovú maticu rozmerov 2x3
- maticu náhodných čísel roznerov 5x3