Špeciálne jazykové prostriedky počítačov - SJPP

9. Práca s funkciami v Matlabe

Funkcia Opis
fminbnd minimalizácia funkcie s jednou premennou
fminsearch minimalizácia funkcie s niekoľkými premennými
fplot zobrazenie priebehu funkcie
fzero nájdenie núl funkcie s jednou premennou
ode23 riešenie diferenciálnych rovníc RK 3. radu
ode45 riešenie diferenciálnych rovníc RK 5. radu
quad numerický integrál v tvare nižšieho rádu

9.1. Minimalizácia funkcií a hľadanie nulového bodu

Pomocou funkcie fminbnd(F,x1,x2) je možné nájsť lokálne minimum funkcie s jednou premennou a menom F na inervale (x1,x2).

Pomocou funkcie fminsearch(F,x0) je možné nájsť najbližšie lokálne minimum funkcie s viacerými premennými a menom F pre začiatočný vektor x0.

9.1.1. Nastavenie položiek minimalizácie

Proces minimalizácie je možné ovplyvniť nastavením riadiacich položiek minimalizácie (options) a použiť nasledovný zápis funkcie fminbnd alebo fminsearch

fminbnd(F,x1,x2,options) alebo fminsearch(F,x0,options)

options je vektor o dĺžke 18. Automatické nastavenie je možné previesť zápisom:

options = foptions;

Príklad 9.1: Jednoparametrová funkcia jedno_par.m
function y = jedno_par(x)
% Jednoparametrova funkcia 
% f(x) = 1/((x-0.3)2+0.01) + 1./((x-0.9)2+0.04) - 6 

y = 1./((x-0.3).^2+0.01) + 1./((x-0.9).^2+0.04) - 6;
Príklad 9.2: Minimum jednoparametrovej funkcie
>> fminbnd('cos',3,4)            % minimum na intervale <3,4>
ans =
    3.1416

>> fminbnd('jedno_par',0.3,1)    % minimum na intervale <0.3,1>
ans =
    0.6370

Poznámka: pri hľadaní minima viacparametrovej funkcie musí mať funkcia iba jeden argument (napr. vektor).
Správne: y = funkcia(x).
Nesprávne: y = funkcia(x1,x2).

Príklad 9.3: Dvojparametrová funkcia dvoj_par.m
function y = dvoj_par(x)
% Dvojparametrova funkcia 
% f(x) = (x1-10)2 + (x2-5)2 - 25 

y = (x(1)-10).^2 + (x(2)-5).^2 - 25;
Príklad 9.4: Minimum dvojparametrovej funkcie
>> fminsearch('dvoj_par',[0,0])      % zaciatocne hodnoty [0,0]
ans =
   10.0000    5.0000

>> fminsearch('dvoj_par',[20,10])    % zaciatocne hodnoty [20,10]
ans =
   10.0000    5.0000
Príklad 9.5: Nulový bod funkcie
>> fzero('sin',3)    		% nulový bod v okolí 3
ans =
    3.1416
>> fzero('sin',4)    		% nulový bod v okolí 4
ans =
    3.1416
>> fzero('sin',5)    		% nulový bod v okolí 5
ans =
    6.2832
	
% Spätná kontrola
>> sin(3.1416)
ans =
 -7.3464e-006
 
>> fzero('jedno_par',-0.2)
ans =
   -0.1316

% Spätná kontrola
>> jedno_par(-0.1316)
ans =
  4.3418e-004
top

9.2. Zobrazenie priebehu funkcie

Pomocu funkcie fplot(fmeno,limit) sa zobrazuje priebeh funkcie s názvom fmeno v zadanom rozsahu limit.

Príklad 9.6: Vykreslenie funkcie jedno_par
>> fplot('jedno_par',[-3,3])
Výsledok príkladu 9.6:
Príklad 9.7: Vykreslenie funkcií sin(x) a cos(x)
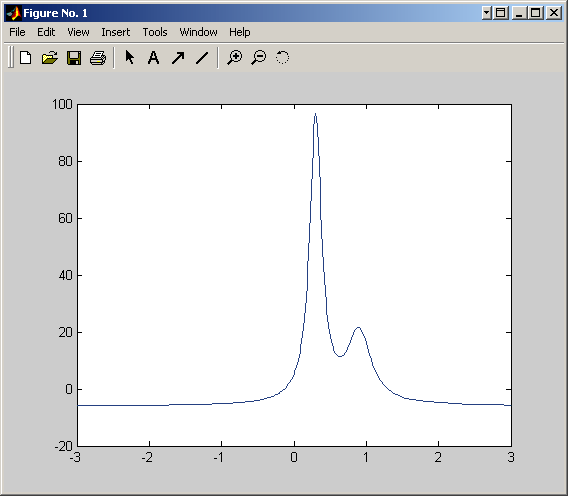
>> fplot('[sin(x), cos(x)]',[0 4*pi])
Výsledok príkladu 9.7:
top

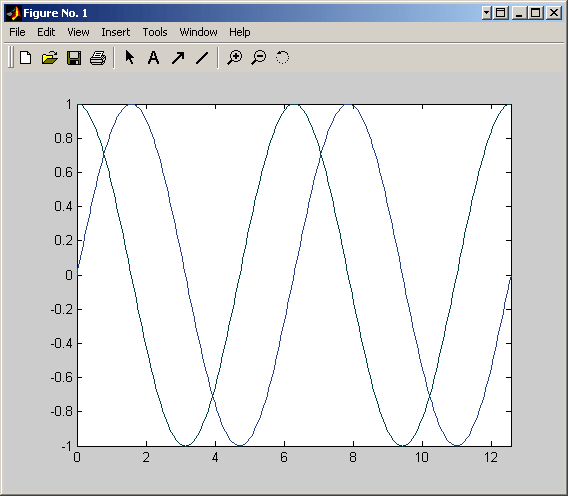
9.3. Riešenie diferenciálnych rovníc

Na riešenie diferenciálnych rovníc je možné použiť funkcie ode23, ode45 a ďalšie.

Syntax príkazu: ode23
[T,Y]=ode23('funkcia',[t0 tfinal],y0)
Funkcia rieši differenciálnu rovnicu opísanú vo funkcii funkcia. Parametre t0 a tfinal predstavujú začiatočný a koncový čas integrácie a y0 je vektor začiatočných hodnôt.

Majme diferenciálnu rovnicu: y''' + 3y'' + 3y' + y = 1
so začiatočnými podmienkami y(0) = 0, y'(0) = 1, y''(0) = -1

Zadefinujme si (rozložme diferenciálnu rovnicu 3. rádu na diferenciálne rovnice 1. rádu): 

y1 = y
y2 = y'
y3 = y''
dy3/dt = - 3y3 - 3y2 - y1 + 1

Potom funkcia v matlabe je v tvare:

Príklad 9.8: Funkcia fundif.m
function dydt = fundif(t,y)
% Diferencialna rovnica: y''' = - 3y'' - 3y' - y + 1
% dydt = [y'; y''; y'''] 
% Vektorovy zapis
% dydt = [y(2); y(3); -3y(3)-3y(2)-y(1)+1]) 

dydt = [y(2); y(3); - 3*y(3) - 3*y(2) - y(1) + 1];
Príklad 9.9: Riešenie diferenciálnej rovnice fundif pomocou ode45
>> [t,y] = ode45('fundif',[0 10],[0 1 -1]);

>> subplot(2,1,1);   % vykreslenie
>> plot(t,y(:,1));
>> subplot(2,1,2);
>> plot(t,y);
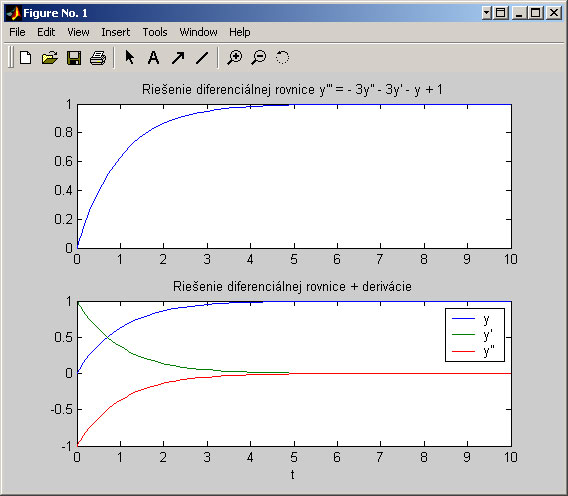
Príklad 9.10: Riešenie algebraickej rovnice (dy/dt = 0)
>> [t,y] = ode45('fundif',[0 10],[0 1 -1]);
% riesenie = y(t1), kde t1->infinity, resp. t1 je cas v ustalenom stave
>> riesenie = y(end,1)    
riesenie =
    1.0000
top

9.4. Numerická integrácia

Zápis funkcie pre výpočet určitého integrálu funkcie funkcia s hranicami a, b, toleranciou tol:

Syntax príkazu: quad
[Q,FCNT] = quad('funkcia',a,b,tol,trace)
Ak číslo trace je rôzne od nuly, tak sa zobrazia aj hodnoty [fcnt a b-a Q].

Príklad 9.11: trace = 1
>> quad('sin',0,pi,1e-5,1)
       9     0.0000000000    8.53193733e-001     0.3424195349
      11     0.8531937329    1.43520519e+000     1.3151544267
      13     0.8531937329    7.17602594e-001     0.6575803480
      15     1.5707963268    7.17602594e-001     0.6575803480
      17     2.2883989207    8.53193733e-001     0.3424195349
ans =
    2.0000
Príklad 9.12: trace = 0
>> quad('sin',0,pi,1e-5,0)
ans =
    2.0000
Príklad 9.13: Vytvorenie funkcie funkcia.m
function f = funkcia(t)
f = sqrt(4*cos(2*t).^2 + sin(t).^2 + 1);
Príklad 9.14: Výpočet integrálu na intervale <0,3pi>
>> quad('funkcia',0,3*pi)
ans =
   17.2220
top

9.5. Úlohy

  1. Vytvorte jednoparametrovú matematickú funkciu f(x) = (x-10)2 + (x-5)2 - 25
  2. S vytvorenou funkciou vykonajte nasledovné úkony:
    • zobrazte jej priebeh na intervale <0,15>
    • nájdite jej lokálne minimum
    • nájdite jej nulový bod
    • vypočítajte numerický integrál funkcie na intervale <0,15>
  3. Vytvorte dvojparametrovú matematickú funkciu f(x,y) = x.*exp(-x.^2-y.^2), nájdite jej minimum
  4. Pomocou funkcie quad riešte integrály:
    • integrál (ex.sin(x) dx) na intervale (0,2)
    • integrál (x2.ex dx) na intervale (3,5)
  5. Pomocou funkcie ode23 riešte diferenciálne rovnice:
    • y'' + 2y' + 2y = 0, y(0) = 1, y'(0) = 1
    • y'' - 4y' + 3y = 2, y(0) = 1, y'(0) = -3
top